Inflatable mattress
A boy jumps off a 10 meters building onto an inflatable mattress. Considering that the human body can handle 10-G deceleration without any injury, what is the minimum thickness can the mattress be? Give your answer to the nearest centimeters.
(Neglect air resistance and assume that the deceleration is constant through the mattress)
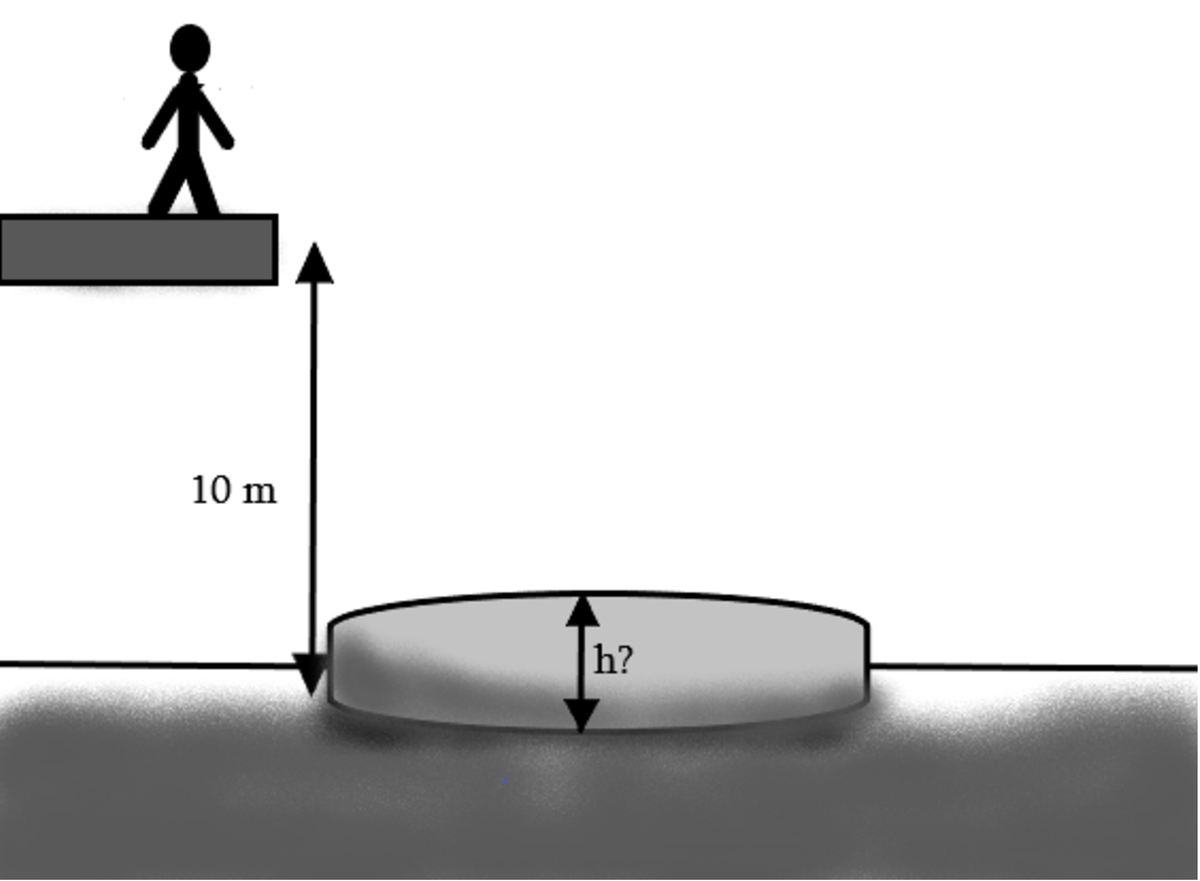
The answer is 91.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Let the minimum thickness of the mattress be h and the velocity when the hit the mattress be v h . By the conservation of energy, we have 2 1 m v h 2 = m g ( 1 0 − h ) , where m is the mass of the boy and g is the acceleration due to gravity. Then we have v h 2 = 2 g ( 1 0 − h ) .
After hitting the mattress, the initial velocity of the boy v h is to be decelerated by a 1 0 − G force until 0 when he reach the ground level. Then we have v h 2 = − 2 0 g h and that:
2 g ( 1 0 − h ) 1 1 h ⟹ h = 2 0 g h = 1 0 = 1 1 1 0 m ≈ 9 1 c m
Discussion: . But I think the deceleration force through the mattress should be 9-G instead of 10-G, because if the deceleration force is 10-G + the gravitational force of 1-G, the poor boy is taking a total of 1-G which may kill him. If net 9-G deceleration is considered the answer is a perfect 1 0 0 c m .