Infographic
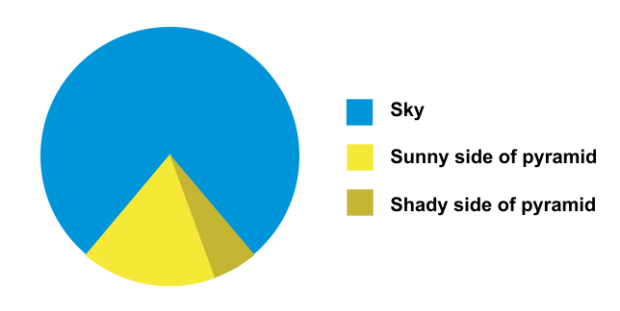
Consider the pie chart shown above, where the ratio of angles formed by the 3 sectors are 3 : 1 4 : 1 . In degrees, what is the measure of angle formed for the sector that represents the shady side of the pyramid?
Image Credit: Flowing Data .
The answer is 20.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
6 solutions
Same thought process. BTW, Why is this a combinatorics problem? I think this should be in Geometry or Algebra.
Since the ratio is 3 : 1 4 : 1 , the total is 3 + 1 4 + 1 = 1 8
It is obvious in the drawing that the shady side is the smallest, so the angle is
1 8 1 ( 3 6 0 ) = 2 0 ∘
3:14:1=18
But you want all the angles to equal 360
18*x=360
x=20
So you times all the ratios by 20
(3)(20) : (14)(20) : (1)(20) = 360
60 : 280 : 20 = 360
Since you are looking for the shady side of the pyramid and since the shady side is the smallest, it means that it is the smallest number
Answer= 20
The shady side of the pyramid equals to ( 3 + 1 4 + 1 ) 3 6 0 × 1 = 1 8 3 6 0 = 2 0 ∘
t o t a l = 3 + 1 4 + 1 = 1 8
s h a d y p a r t o f p y r a m i d = ( 1 8 1 ) ( 3 6 0 ) = 2 0 d e g r e e s
a circle=360° 3(sunny side)+14(sky)+1(shady)=18 =360÷18=20 =1=20 shady side of the pyramind=20(%)
Let the angles be 1 4 x , 3 x and x representing sky,sunny side of the pyramid and shady side of the pyramid respectively.Then we have that 1 4 x + 3 x + x = 3 6 0 ⟹ 1 8 x = 3 6 0 ∴ x = 2 0 . Therefore the angle formed by the shady side of the pyramid is 2 0 ° .