Injection between finite sets

Probability Level 3

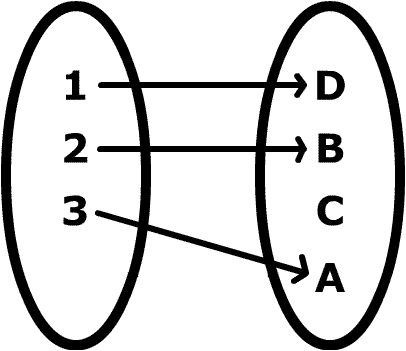Let A A be a finite set ∣ A ∣ = n |A| = n , and B B a finite set as well, with ∣ B ∣ = m > n |B| = m > n . How many injective function f : A → B f : A \rightarrow B are there?

n m n^m n ( n − 1 ) ⋯ ( n − m + 1 ) n(n-1)\cdots(n-m+1) m n m^n n × m n \times m m ( m − 1 ) ⋯ ( m − n + 1 ) m(m-1)\cdots(m-n+1) infinitely many

Patrick Bourg by Patrick Bourg , 28, United Kingdom

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

1 solution

Patrick Bourg
Feb 9, 2015

The number of injective functions is m ( m − 1 ) ⋯ ( m − n + 1 ) m(m-1)\cdots(m-n+1) . This is because, you have m m choices for the first element in A, m − 1 m-1 choices for the second one, etc. Note that this formula is also acceptable if n > m n>m , because it gives 0, which it should!

1 Helpful 0 Interesting 0 Brilliant 0 Confused

The formula I came up with was m!/(m-n)! but I guess it's ultimately the same result.

Tristan Goodman - 11 months, 2 weeks ago

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...