INMO Problem!
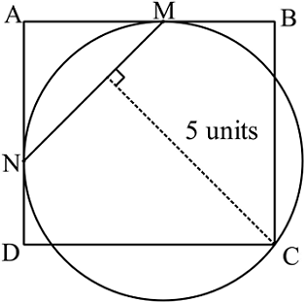
A circle passes through the vertex C of a rectangle A B C D and is tangent to the sides A B and A D at M and N respectively. If the distance from C to the line segment M N is equal to 5 units, find the area of the rectangle A B C D in unit 2 .
The answer is 25.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
Nice approach, I too solved by similariry of triangles.
Log in to reply
same thing even I did.see my solution.
Let O be the center of circle ( C M N ) and Q the midpoint of M N . Since the circle is tangent to A B and A D at M and N respectively, we have ∠ M O N = 9 0 ∘ ⇒ ∠ M C N = 4 5 ∘ ⇒ ∠ Q C M = 2 2 . 5 ∘ and ∠ M C B = 2 2 . 5 ∘ . Since ∠ M Q C = ∠ M B C = 9 0 ∘ , it follows that triangles M Q C and M B C are congruent. Hence, B C = 5 , Area = 5 2 = 2 5 u n i t s 2
Good observation!
good one !!!!
sir how can we say area = AC^2 /2
The "diagonals" method.
The area of a square is half the product of the diagonals.
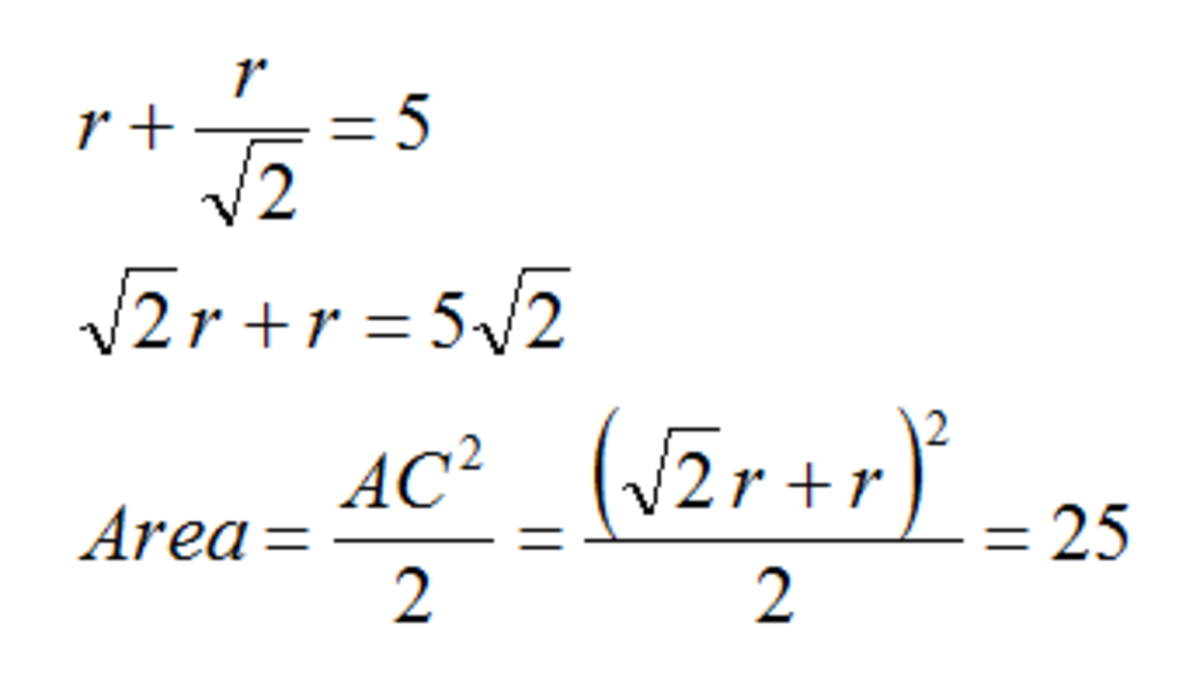
Let P be the foot of perpendicular from C to M N .
Since B M is a tangent to the circle ,
∠ D N C = ∠ N M C
⇒ s i n ∠ D N C = s i n ∠ N M C
⇒ C N D C = C M C P
⇒ C P D C = C M C N
Similarly C P C B = C N C M
Multiplying these two relations,we get D C × C B = C P 2 = 5 2 = 2 5 ; i . e . , the area of the rectangle is 2 5 s q . u n i t s .