Inner 6-7-8 triangle

There exists a point inside a triangle such that it is 6, 7 and 8 units away from the triangle's vertices.
Let the side lengths of this triangle be denoted as a , b and c as shown above.
Among all the possible ways to construct such a triangle above, the largest possible perimeter can be obtained when a , b , c satisfy the equation a 2 + a 2 P 2 + Q = b 2 + b 2 R 2 = c 2 + c 2 S 2 + T ,
where P , Q , R , S , T are constant positive integers. What is P + Q + R + S + T ?
Inspiration . I was trying to find the closed form of p there but I went into a rabbit hole and formulated this question.
The answer is 138.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
Let A , B , C , P be points in the plane such that x = A P , y = B P , z = C P are fixed distances. Then by the arguments in the following links, when the perimeter of triangle A B C is maximized, P is the incenter of triangle A B C .
https://www.cut-the-knot.org/Curriculum/Geometry/TripolarOptimization.shtml
Let r be the inradius of triangle A B C . Then r is the height of triangle P B C with respect to base B C , so by Heron's formula, r 2 = ( B C 2 [ P B C ] ) 2 = a 2 4 [ P B C ] 2 = 4 a 2 ( ( y + z ) 2 − a 2 ) ( a 2 − ( y − z ) 2 ) = 4 a 2 − a 4 + 2 ( y 2 + z 2 ) a 2 − ( y 2 − z 2 ) 2 . Then − 4 r 2 = a 2 − 2 ( y 2 + z 2 ) + a 2 ( y 2 − z 2 ) 2 .
Likewise, − 4 r 2 − 4 r 2 = b 2 − 2 ( x 2 + z 2 ) + b 2 ( x 2 − z 2 ) 2 , = c 2 − 2 ( x 2 + y 2 ) + c 2 ( x 2 − y 2 ) 2 , so a 2 − 2 ( y 2 + z 2 ) + a 2 ( y 2 − z 2 ) 2 = b 2 − 2 ( x 2 + z 2 ) + b 2 ( x 2 − z 2 ) 2 = c 2 − 2 ( x 2 + y 2 ) + c 2 ( x 2 − y 2 ) 2 .
Plugging in x = 8 , y = 6 , z = 7 gives us a 2 − 1 7 0 + a 2 1 3 2 = b 2 − 2 2 6 + b 2 1 5 2 = c 2 − 2 0 0 + c 2 2 8 2 , which leads to a 2 + a 2 1 3 2 + 5 6 = b 2 + b 2 1 5 2 = c 2 + c 2 2 8 2 + 2 6 .
Let
θ
1
,
θ
2
and
θ
3
denote the interior angles that split the original triangle into 3 triangles.
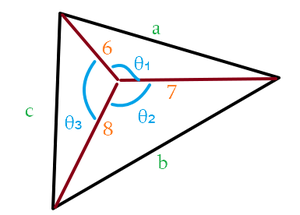
By cosine rule , cos θ 1 = 8 4 8 5 − a 2 cos θ 2 = 1 1 2 1 1 3 − b 2 cos θ 3 = 9 6 1 0 0 − c 2
We want to maximize P : = a + b + c = 8 5 − 8 4 cos θ 1 + 1 1 3 − 1 1 2 cos θ 2 + 1 0 0 − 9 6 cos θ 3
Note that cos ( θ 3 ) = cos [ 2 π − ( θ 1 + θ 2 ) ] = cos ( θ 1 + θ 2 ) = cos ( θ 1 ) cos ( θ 2 ) − sin ( θ 1 ) sin ( θ 2 ) .
Thus, we can express P as a two variable function (in terms of θ 1 and θ 2 ). When P is maximized, its partial derivatives are both equal to 0 , ∂ θ 1 ∂ P = 0 , ∂ θ 2 ∂ P = 0 .
∂ θ 1 ∂ P = 0 ⟹ 1 0 0 − 9 6 cos ( θ 1 + θ 2 ) 4 8 sin ( θ 1 + θ 2 ) + 8 5 − 8 4 cos θ 1 4 2 sin θ 1 = 0 ( 1 )
∂ θ 2 ∂ P = 0 ⟹ 1 0 0 − 9 6 cos ( θ 1 + θ 2 ) 4 8 sin ( θ 1 + θ 2 ) + 1 1 3 − 1 1 2 cos θ 2 5 6 sin θ 2 = 0 ( 2 )
Because ( 1 ) = ( 2 ) :
8 5 − 8 4 cos θ 1 4 2 sin θ 1 = 1 1 3 − 1 1 2 cos θ 2 5 6 sin θ 2
Square both sides of the equation, then utilize the identity sin 2 ( Z ) = 1 − cos 2 ( Z ) ,
a 2 9 [ 1 − ( 8 4 8 5 − a 2 ) 2 ] = b 2 1 6 [ 1 − ( 1 1 2 1 1 3 − b 2 ) 2 ]
Upon simplifying, a 2 + a 2 1 6 9 + 5 6 = b 2 + b 2 2 2 5 . ( 3 )
Likewise we can also express P as a two variable function (in terms of θ 1 and θ 3 ), and by using cos ( θ 2 ) = cos ( θ 1 + θ 3 ) = cos ( θ 1 ) cos ( θ 3 ) − sin ( θ 1 ) sin ( θ 3 ) .
Using the similar reasoning as above, we gather that
∂ θ 1 ∂ P = 0 ⟹ 1 1 3 − 1 1 2 cos ( θ 1 + θ 3 ) 5 6 sin ( θ 1 + θ 3 ) + 8 5 − 8 4 cos θ 1 4 2 sin θ 1 = 0 ( 4 )
∂ θ 3 ∂ P = 0 ⟹ 1 1 3 − 1 1 2 cos ( θ 1 + θ 3 ) 5 6 sin ( θ 1 + θ 3 ) + 1 0 0 − 9 6 cos θ 3 4 8 sin θ 3 = 0 ( 5 )
Again, because ( 4 ) = ( 5 ) :
8 5 − 8 4 cos θ 1 4 2 sin θ 1 = 1 0 0 − 9 6 cos θ 3 4 8 sin θ 3 ⟹ a 2 4 9 [ 1 − ( 8 4 8 5 − a 2 ) 2 ] = b 2 6 4 [ 1 − ( 9 6 1 0 0 − b 2 ) 2 ]
Simplify once more a 2 + a 2 1 6 9 + 3 0 = c 2 + c 2 7 8 4 ( 6 )
Combining ( 3 ) and ( 6 ) yields
a 2 + a 2 1 6 9 + 5 6 = b 2 + b 2 2 2 5 = c 2 + c 2 7 8 4 + 2 6 .
Hence, P = 1 6 9 = 1 3 , Q = 5 6 , R = 2 2 5 = 1 5 , S = 7 8 4 = 2 8 , T = 2 6 . The answer is 1 3 + 5 6 + 1 5 + 2 8 + 2 6 = 1 3 8 .
Can someone prove the following?
The perimeter of this triangle has a maximum value of approximately 3 6 . 4 5 6 2 when ( a , b , c ) ≈ ( 1 1 . 0 0 7 3 , 1 3 . 3 1 4 9 , 1 2 . 1 3 3 9 ) .
This maximum perimeter of such a triangle is the largest real root to the 6th degree polynomial
7 0 5 6 X 6 − 9 3 7 2 5 2 7 X 4 − 7 0 2 2 6 3 2 X 2 + 2 9 8 1 1 6 0 0
If the central angles are α , β , γ , then a = 8 5 − 8 4 cos α , b = 1 1 3 − 1 1 2 cos β and c = 1 0 0 − 9 6 cos γ , and so we want to maximise a + b + c = 8 5 − 8 4 cos α + 1 1 3 − 1 1 2 cos β + 1 0 0 − 9 6 cos γ subject to the restraint α + β + γ = π . Lagrange multipliers tell us that a 4 2 sin α = b 5 6 sin β = c 4 8 sin γ = k for some contant k , and hence k 2 2 2 6 − 4 k 2 = a 2 4 2 2 [ 1 − ( 8 4 8 5 − a 2 ) 2 ] = b 2 5 6 2 [ 1 − ( 1 1 2 1 1 3 − b 2 ) 2 ] = c 2 4 8 2 [ 1 − ( 9 6 1 0 0 − c 2 ) 2 ] = 4 a 2 ( a 2 − 1 ) ( 1 6 9 − a 2 ) = 4 b 2 ( b 2 − 1 ) ( 2 2 5 − b 2 ) = 4 c 2 ( c 2 − 4 ) ( 1 9 6 − c 2 ) = a 2 + a 2 1 3 2 + 5 6 = b 2 + b 2 1 5 2 = c 2 + c 2 2 8 2 + 2 6 making the answer 1 3 + 5 6 + 1 5 + 2 8 + 2 6 = 1 3 8 .