Inradii Among Us
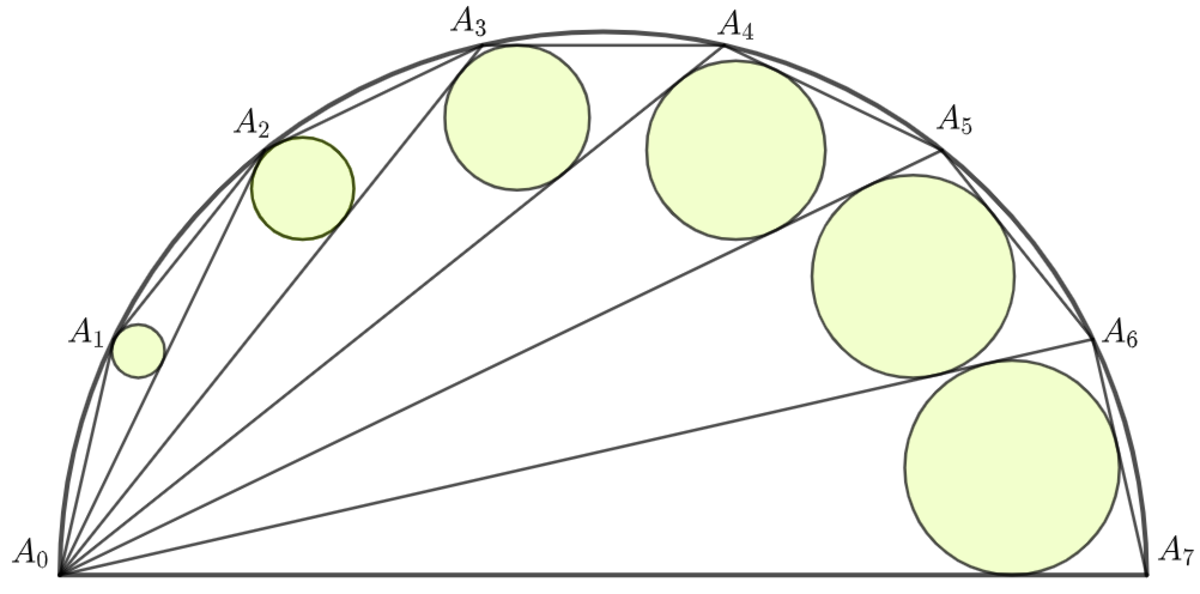
In the semicircle of radius , each of the triangles shares the common vertex . The measurement of , , , , and is radians.
If the area sum of all green incircles is , find the digit sum of .
Inspiration. (And among others!)
The answer is 56.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
The Equation exist for triangle
R r = c o s α + c o s β + c o s γ − 1
r - inradius, R - outradius.
Here 6 triangles with R = 1 and sets of angles α i , β i , γ i
1 . 1 4 π , 1 4 6 π , 1 4 7 π
2 . 1 4 π , 1 4 5 π , 1 4 8 π
3 . 1 4 π , 1 4 4 π , 1 4 9 π
4 . 1 4 π , 1 4 3 π , 1 4 1 0 π
5 . 1 4 π , 1 4 2 π , 1 4 1 1 π
6 . 1 4 π , 1 4 π , 1 4 1 2 π
∑ i = 1 6 S i = π ∑ i = 1 6 r i 2 = π ∑ i = 1 6 ( c o s α i + c o s β i + c o s γ i − 1 ) 2
Use WolframeAlpha to calculate the sum - answer
0 . 4 0 7 6 5 5 2 8 1 3 3 4 5 3 . . . .
5 6
And another way with Python