Inradius of a regular Octahedron
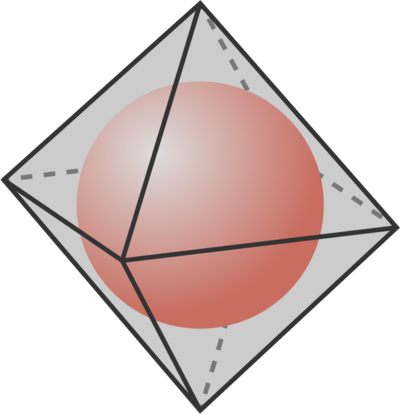
A sphere is inscribed in a regular octahedron.
What is the ratio of the sphere’s radius to the octahedron’s edge length?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
9 solutions
I'm a bit of a noob but why would DB not just be half of AB which is as it is stated above
Log in to reply
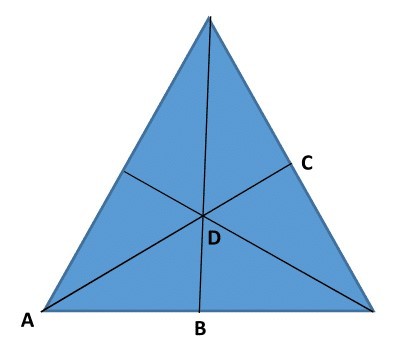 D is in the center of a equilateral triangle.
D is in the center of a equilateral triangle.
A D D C = A D B D = s i n ( 3 0 ∘ ) = 2 1
This means A D = 2 ⋅ D C
Is there any quiz to give the formal definition of an octahedron and it's properties as I do not know what the question is (I thought an octahedron was a polyhedron and do not know what an edge length is)
Log in to reply
The edge length was not given, but since we are only interested in ratio of distances, we can pick whatever value we want for the edge length (it will cancel if called say x ). Usually the thing to do is make it equal to 1 .
When you need to check definitions, Googling them is a good way to go about it. In this case, octahedron is a polyhedron with eight sides, each an equilateral triangle. The image provided is a good in showing its look.
Why is DB 1/3 and not 1/sqrt(3) ?
Log in to reply
 D is in the center of a equilateral triangle.
D is in the center of a equilateral triangle.
A D D C = A D B D = s i n ( 3 0 ∘ ) = 2 1
This means A D = 2 ⋅ D C
I feel it would be better to connect to the definition of inscribed - meaning the sphere is tangent with the face - rather than just stating where D is.
Is AC . CB = AB . CD works?
Log in to reply
It's true, as both are twice the area of the triangle A B C , but I am not sure how you are using this.
Let edge length be 1 . Then the distance from the center of any square to the edge is 2 1 . The distance from the center of any equilateral triangle to the edge is 2 3 1 . Then we have for the inradius
( 2 1 ) 2 − ( 2 3 1 ) 2 = 6 1
It's a well-written solution!
Using a unit octahedron the radius and the ratio are the same number. That number can be found using several steps of basic geometry as shown below.






Thankyou, this has been a most detailed and helpful solution
The diameter of the sphere must be smaller than the length of the edge. So the double of an answer must be smaller than 1 to be valid. There is only one such answer.
A regular octagon is most easily described by placing vertices at the points ( ± 1 , 0 , 0 ) , ( 0 , ± 1 , 0 ) , ( 0 , 0 , ± 1 ) .
The side length is the distance between ( 0 , 1 , 0 ) and ( 1 , 0 , 0 ) (for instance): d = 1 2 + 1 2 = 2 .
The faces may be described by equations of the form ± x ± y ± z = 1 . Symmetry shows that the sphere touches each face at ± x = ± y = ± z , which is therefore equal to 3 1 . This means that the radius of the sphere is r = ( 3 1 ) 2 + ( 3 1 ) 2 + ( 3 1 ) 2 = 1 / 3 . Thus d r = 2 1 / 3 = 6 1 .
To get the radius, we could use formula of distance from ( 0 , 0 , 0 ) to one of the face:
r = 1 2 + 1 2 + 1 2 ∣ ∣ 0 + 0 + 0 − 1 ∣ ∣ = 3 1
Log in to reply
Correct. However, I tried to use no "black box" formulas in the solution.
Just look at one of the face of octahedron, let its side length be 2 a then the length from the center of octahedron to one of its verticle will be a .
Then, by setting the origin of 3d-coordinate system be the center of octahedron, and let x , y , z axis point to three of its verticles, then the plane equation will be x + y + z = a , so the distance from origin to the plane must be r = ∣ ∣ ∣ ∣ 1 2 + 1 2 + 1 2 0 + 0 + 0 − a ∣ ∣ ∣ ∣ = 3 a , after compare, we get the ratio of radius to its side length be 6 1 .
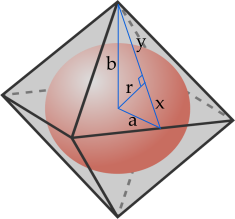
Purely Pythagorean: if side length is 1,
a x + y b r 2 r 2 2 1 − y 2 y r = 2 1 = 2 3 = 2 1 = a 2 − x 2 = 4 1 − ( 2 3 − y ) 2 = y 3 − y 2 − 2 1 = b 2 − y 2 = y 3 − y 2 − 2 1 = 3 1 = 6 1
There isn’t any thing
Not impressed.
You could at least learn enough html to make the link scroll to the appropriate section like this
https://en.wikipedia.org/wiki/Octahedron#Regular_octahedron
Anything less is just rude.
Better yet, you could spare us the sarcasm by deleting your "solution".

Point of contact between the sphere and the octahedron, D is in the center of the face, therefore the median A B is divided in the ration of 2 : 1 making D B = 3 1 ⋅ A B = 2 3 1 .
Triangle C B D has a right angle at D , so C D = C B 2 − D B 2 = 4 1 − 1 2 1 = 6 1 .