Ins and Outs

$Since$ $the$ $vertical$ $angle$ $of$ $Delta$ is $obtuse$ => $The$ $circumcenter$ $will$ $lie$ $only$ $outside$ $the$ $triangle$ .

If angles $B$ and $C$ are equal, then the fact that $R=4$ gives us $a \; = \; 8\sin A \; = \; 8\sin(\pi-2C) \; = \; 8\sin2C$ while the fact that $r=1$ gives us $\frac{2}{a} \; = \; \tan\tfrac12C$ and hence $1 \; = \; 4\tan\tfrac12C \sin2C$ Putting $x = \tan\tfrac12C$ , we deduce that $\begin{aligned} (1 + x^2)^2 & = \; 16x^2(1-x^2) \\ 17x^4 - 14x^2 + 1 & = 0 \end{aligned}$ and hence $x \; = \; \sqrt{\frac{7 \pm 4\sqrt{2}}{17}}$ When $x = \sqrt{\frac{7 + 4\sqrt{2}}{17}}$ all the angles in the triangle are acute. When $x = \sqrt{\frac{7 - 4\sqrt{2}}{17}}$ the angle $A$ is obtuse, and the longest side is $a = \boxed{7.11529}$ .

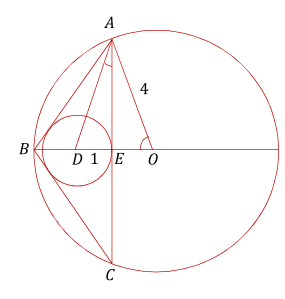In the figure, $D$ is a center of the incircle and $O$ center of the circumcircle of triangle $ABC$ with $AB=BC$ .

Let’s have $\gamma=\angle DAE=\angle DAB$ . Angle $ABO=90^\circ-2\gamma.$ Angle $AOB=2\times(90^\circ-\angle ABO)=4\gamma$ .

From triangle $AEO, AE=4\times sin(4\gamma)=8 sin(2\gamma) cos(2\gamma)=16 sin(\gamma) cos(\gamma)(1-2 sin^2(\gamma)).$

From triangle $AED, AE=\frac{1}{tan(\gamma)}$ .

Combining the two and simplifying: $sin^2(\gamma)(1-2 sin^2(\gamma))=\frac{1}{16}$

Solving: $sin^2(\gamma)=\frac{2-\sqrt{2}}{8}$

$\gamma=15.7^\circ, 4\gamma=62.8^\circ$

$AE=4\times sin(4\gamma)=3.5576$ . So the longest side of triangle $ABC$ is double that or approximately $7.115$ .

It is easy to show that sides $AB=BC=2\times 4\times sin(2\gamma)=4.17$ are smaller.

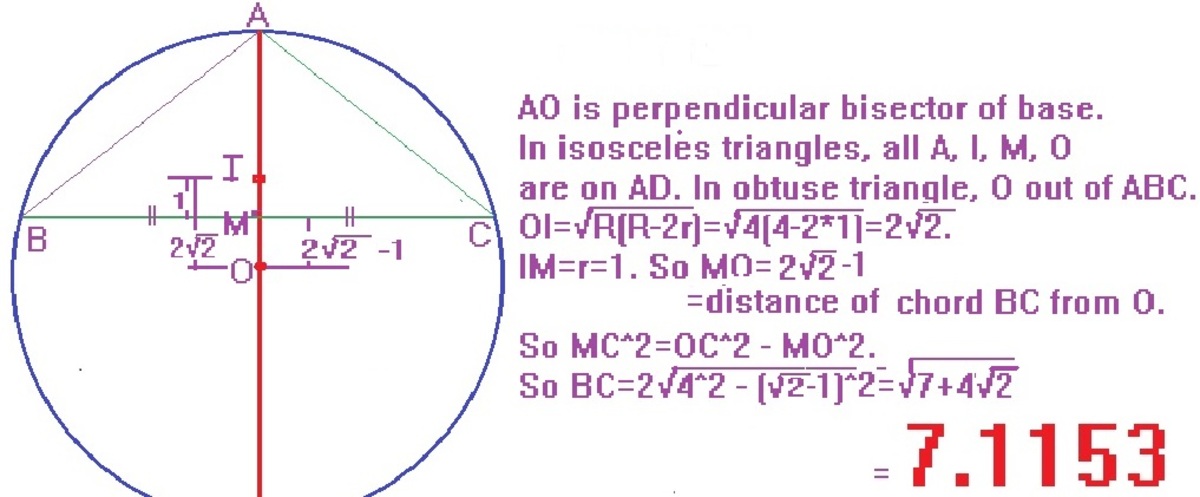
OR

$Distance~between~two~centers~=\sqrt{R(R-2r)}=2\sqrt2.\\ \therefore~distance~between~ circumcenter ~and~midpoint~of~the~base~=2\sqrt2 - 1=half~the~base~which ~is~also~the~chord~of~circumcircle.\\ \therefore~half~base=\sqrt{4^2-(2\sqrt2 - 1)^2}.\\ For~an~obtuse~ isosceles~ triangle~the~base~is~the~largest~side=~2*\sqrt{4^2-(2\sqrt2 - 1)^2}=~\color{#D61F06}{7.1153}.$