Inscribe-ception

Geometry Level 1

Draw a $1\text{ m}$ by $1\text{ m}$ square.
Then inscribe the largest possible circle within the square previously drawn.
Then inscribe the largest possible square within the circle previously drawn.
Then inscribe the largest possible circle within the square previously drawn.
Then inscribe the largest possible square within the circle previously drawn.
Then repeat the process indefinitely.

What will be the total area of all the squares drawn (in $\text{m}^2$ )?

The answer is 2.

3 solutions

Wee Xian Bin
Jul 9, 2016

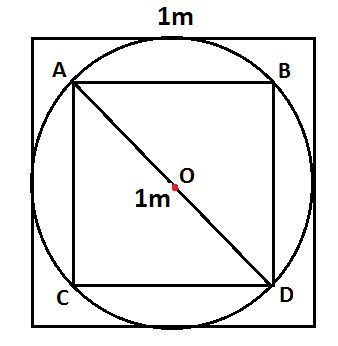
If every alternate square was tilted diagonally the above figure is obtained.

It can then be determined that the area of each successive square would be half the area of the previous square.

Therefore the total area of all the squares drawn is $1+\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\frac{1}{16}+...=\frac{1}{1-\frac{1}{2}}=2$ sq m.

If a square is 1 x1 m, then how can areas inscribed be more than 1m²? Thanks

D.j. Diepen - 4 years, 9 months ago

That's a fair point. However, try to do it subtracting the area of the circles. I will tell you the answer is about 0.429.

Saúl Huerta - 1 year, 7 months ago

"The total area of all the squares drawn"

Wee Xian Bin - 4 years, 8 months ago

I got it wrong somehow and this is what i got, although It asks for the answer in sq cm so I put 20000cm^2 instead of 2m^2

Calum Campbell - 4 years, 11 months ago

Have changed it back to square metres, when I originally posted this question I did put square metres so I'm not quite sure what happened...

Wee Xian Bin - 4 years, 11 months ago

Why have you nat substracted the area of circles??

Rounak Chourasia - 4 years, 8 months ago

"The total area of all the squares drawn"

Wee Xian Bin - 4 years, 8 months ago

What's the principle when we add 1+1/2+1/4.... and get 2?

Abusha Vopalat - 4 months, 1 week ago

Betty BellaItalia
Jan 6, 2018

Alkis Piskas
Oct 23, 2018

In the above figure, we can see that the first inscribed circle has a radius 0.5m, so its diameter is 1m. From the right triangle ACD, we have 2 * AC^2 = 1^2 = 1 => AC^2 = 1 / 2 , with AC being the side of the first inscribed square ABCD and equal to the diameter of the next inscribed circle. So if we continue this process, the sum of all squares will be 1 + 1/2 + 1/4 + ... which tends to 2 .

Inscribe-ception

The answer is 2.

3 solutions

0 pending reports