Inscribed and Circumscribed Spheres 3
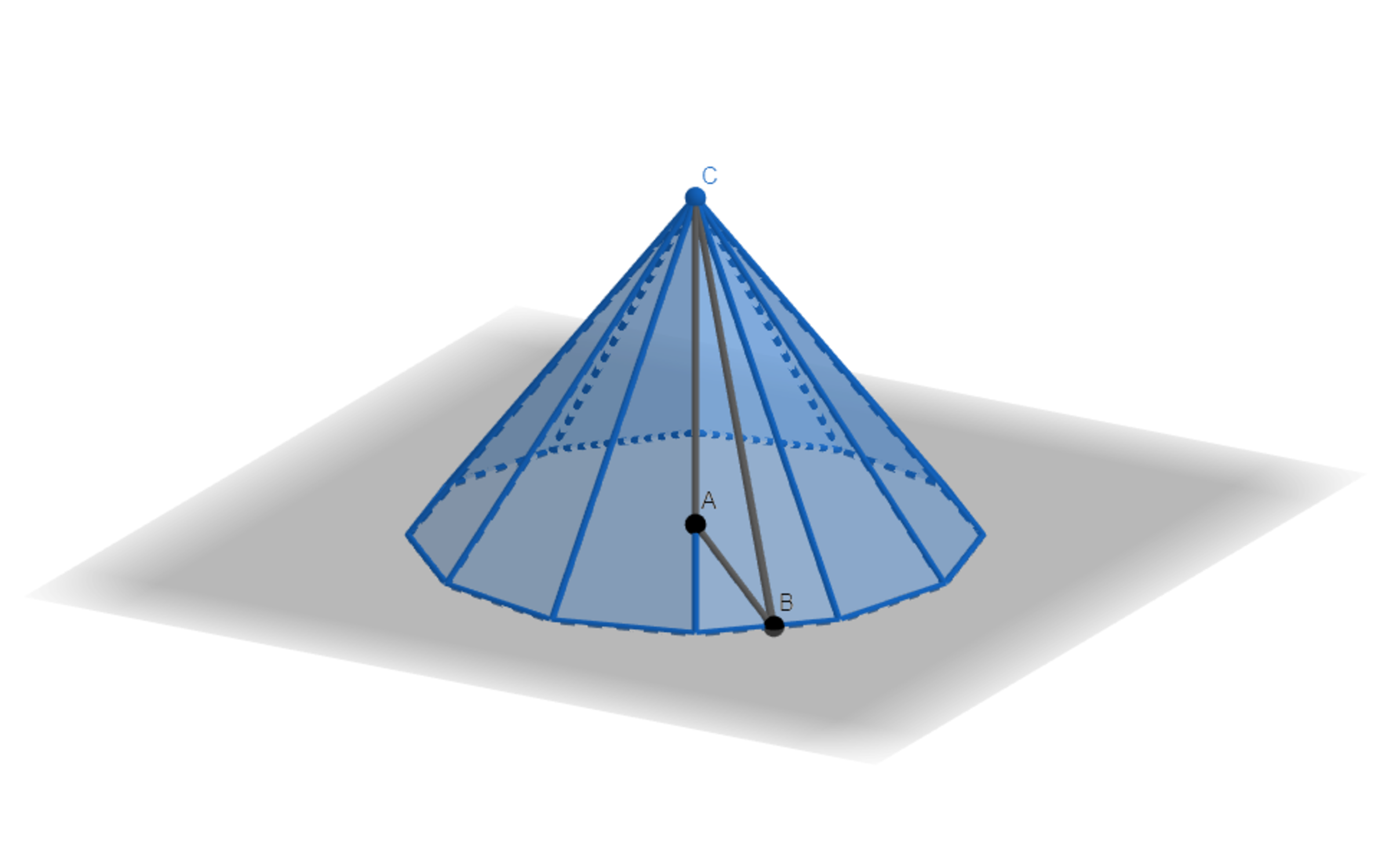
A sphere is inscribed in a -gonal pyramid whose base is a regular -gon, where is a positive integer and .
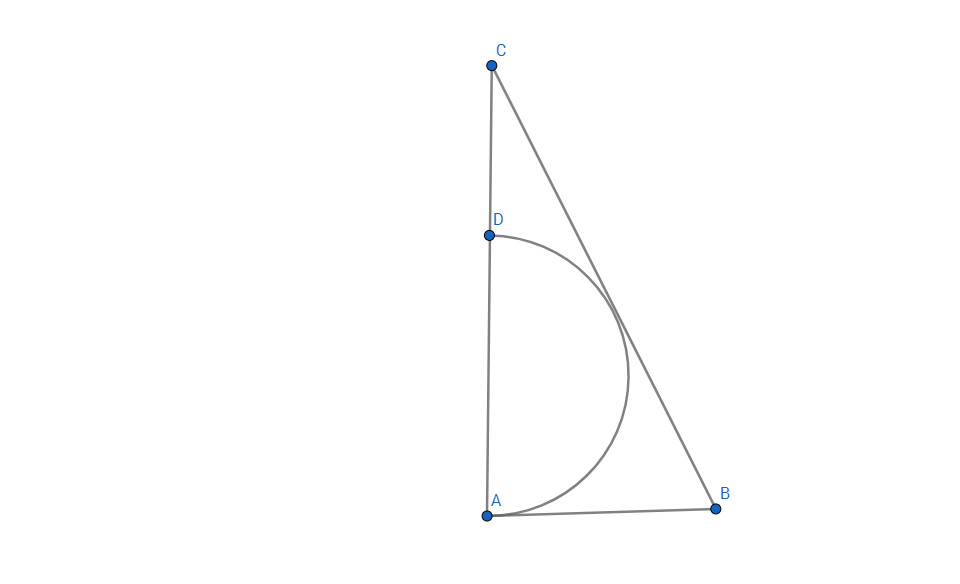
In right let be the radius of the inscribed sphere, the height of the pyramid and a positive real number.
The side of the base of the -gonal pyramid is , the slant height , and .
Inscribe the given -gonal pyramid in a sphere and let be the volume of the circumscribed sphere. Let be the volume of the inscribed sphere.
Find
Note: .
The answer is 8.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
For area of n − g o n :
Let P Q = x be a side of the n − g o n , P B = Q B = m , A B = h ∗ , and ∠ Q B A = n π .
2 x = m sin ( n π ) ⟹ m = 2 sin ( n π ) x ⟹ h ∗ = 2 x cot ( n π ) = 2 r j cot ( n π )
In right △ A B C O E ⊥ B C , O E = O D = O A = r , O C = r + j , A B = h ∗ = 2 r j cot ( n π ) ⟹ E B = 2 r j cot ( n π ) and let C E = y .
△ A B C ∼ △ C O E ⟹ 2 j cot ( n π ) = 2 ( r + j ) r j cot ( n π ) + 2 y ⟹ r j cot ( n π ) + j 2 cot ( n π ) = r j cot ( n π ) + 2 y ⟹ y = 2 j 2 cot ( n π ) .
In right △ C O E the pythagorean theorem ⟹ 4 j 4 cot 2 ( n π ) + r 2 = r 2 + 2 r j + j 2 ⟹ j 4 cot 2 ( n π ) = 8 r j + 4 j 2 ⟹ r = ( 8 j 2 cot 2 ( n π ) − 4 ) j ⟹
h = A C = 2 r + j = 4 j 3 cot 2 ( n π ) and h ∗ = A B = 1 6 ( j 2 c o t ( n π ) − 4 ) cot ( n π )
In △ A B C the pythagorean theorem ⟹ s = B C = 1 6 j 2 cot ( n π ) ( j 2 cot 2 ( n π ) + 4 ) = 4 5 j 2 cot ( n π ) = 1 6 2 0 j 2 cot ( n π ) ⟹
1 6 j 2 cot ( n π ) ( j 2 cot ( n π ) − 1 6 ) = 0 ⟹ j = 4 tan ( n π ) for j > 0 ⟹ r = 2 tan ( n π ) ( 4 − tan 2 ( n π ) ) .
For the circumscribed sphere:
Let O be center of the circumscribed sphere and R be the radius.
In right △ A O H , A H = m , O A = h − R , and O H = R ⟹
( h − R ) 2 + m 2 = R 2 ⟹ h 2 − 2 h R + m 2 = 0 ⟹ R = 2 h m 2 + h 2
From above m = 2 sin ( n π ) r j = 4 sec ( n π ) tan ( n π ) ( 4 − tan 2 ( n π ) ) and h = 1 6 tan ( n π ) ⟹ R = 2 ( tan ( n π ) ) [ ( 4 − tan 2 ( n π ) ) 2 sec 2 ( n π ) + 1 6 ]
r ( n ) R ( n ) = 4 ( 4 − tan 2 ( n π ) ) ( 4 − tan 2 ( n π ) ) 2 sec 2 ( n π ) + 1 6 and lim n → ∞ r ( n ) R ( n ) = 2 ⟹ lim n → ∞ V 1 ( n ) V 2 ( n ) = 2 3 = 8 .