Inscribed and Tangent
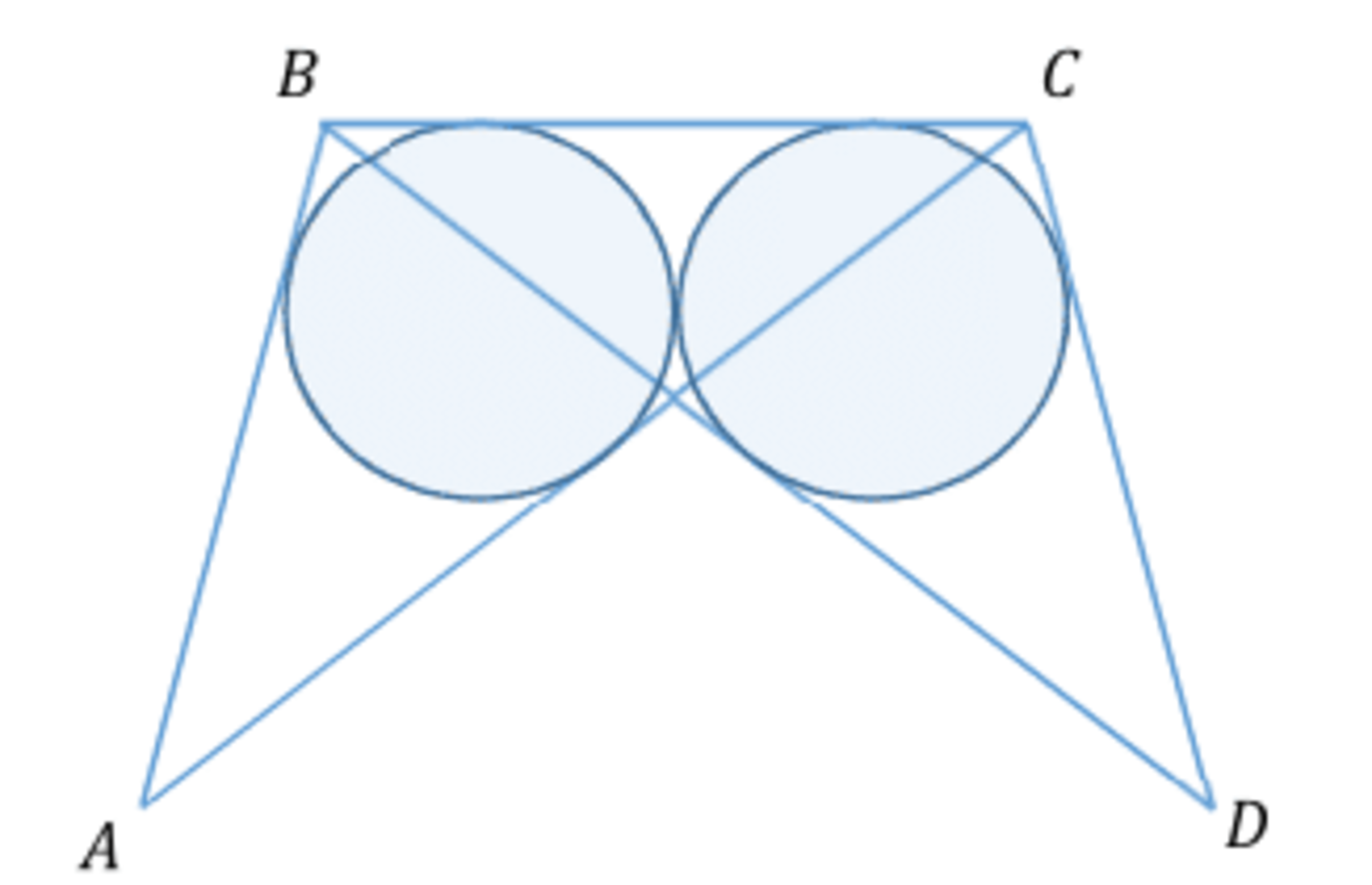
Two congruent isosceles triangles and share the side , , and their incircles are tangent to each other. Find the angle in degrees.
The answer is 101.736.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Also R + x = 2 1 and x R = t a n ( α ). So we have t a n ( α ) R + R = 2 1 . This will give us R = 2 ( s i n ( α ) + c o s ( α ) ) s i n ( α )
Setting the two expressions for R equal to each other, we get 1 + s i n ( α ) c o s ( α ) = 2 ( s i n ( α ) + c o s ( α ) ) 1 .
Introducing y = s i n ( α ) we can write this equation as 1 + y 1 − y 2 = 2 ( y + 1 − y 2 ) 1 .
The applicable solution is y = 0 . 7 7 5 6 9 , giving us α = 5 0 . 8 6 8 ∘
The ∠ A B C = ∠ B C D = 2 × α = 1 0 1 . 7 3 6 ∘ .