Can You Find the Area?
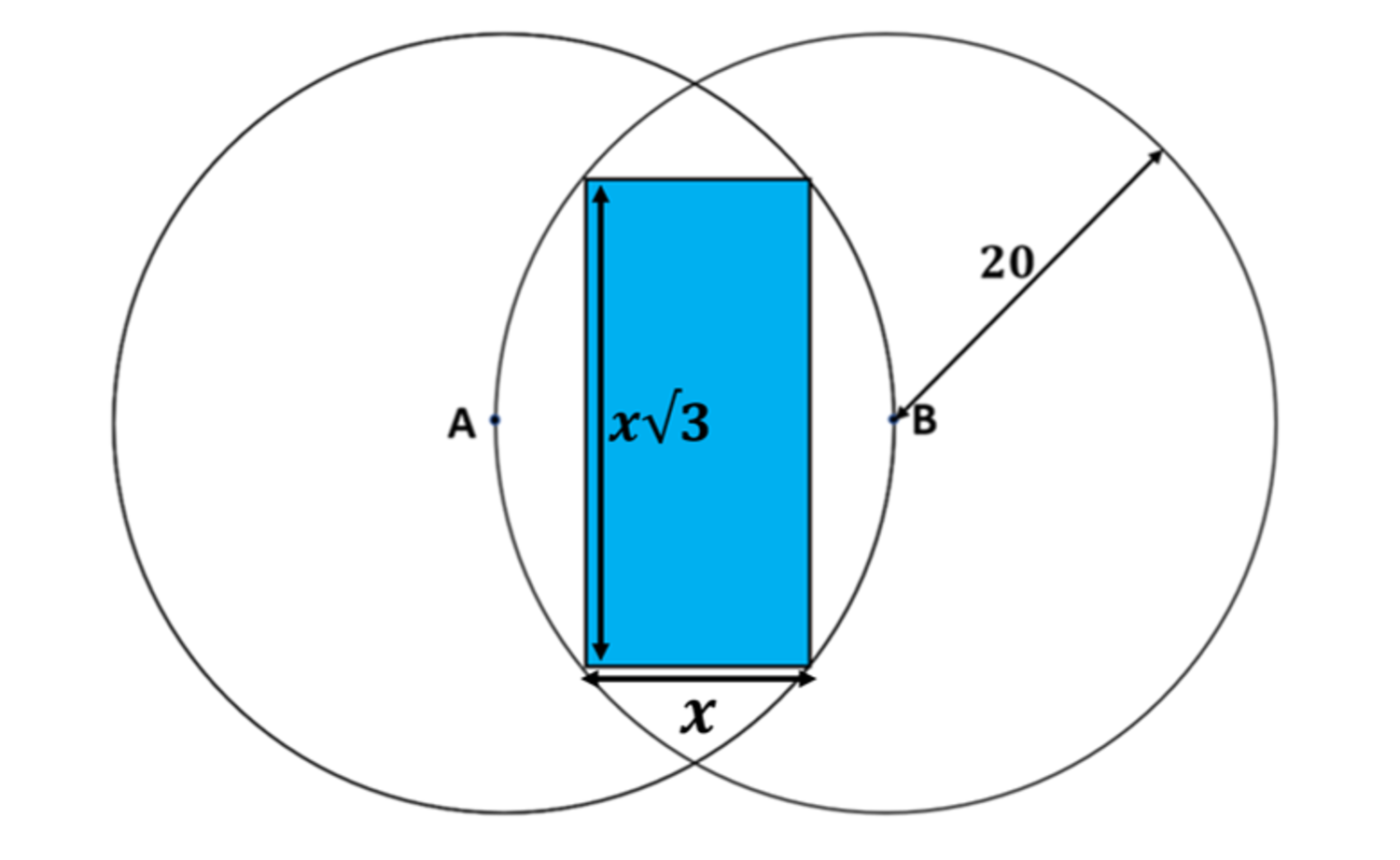
Two circles of radius 2 0 have centres at points A and B . Point A lies on the right circle and point B lies on the left circle. A rectangle with side lengths x and x 3 is inscribed in the intersection of the two circles as shown.
What is the area of the rectangle to three significant digits?
The answer is 294.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
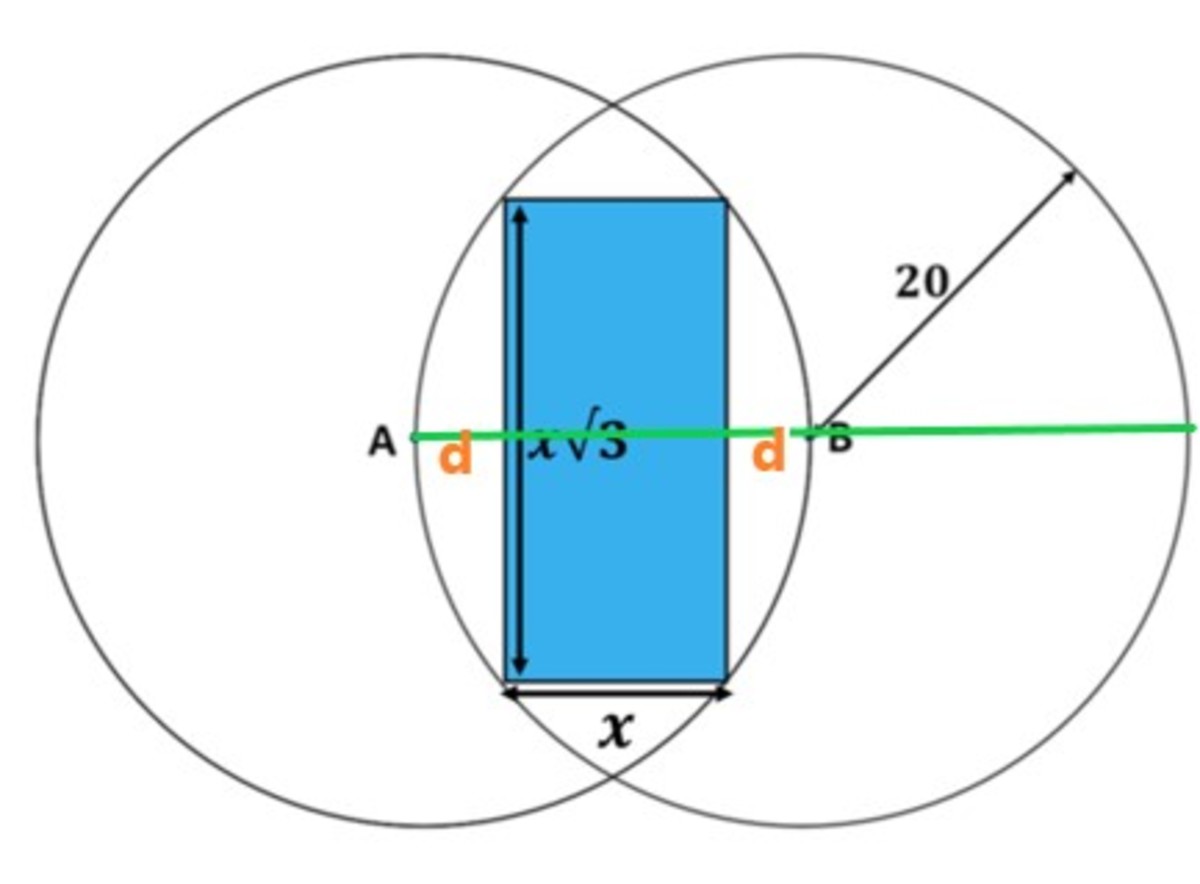
By symmetry, we can find d = 2 2 0 − x
By Intersecting chord theorem ,
( 2 3 x ) 2 = d × ( d + x + 2 0 ) 3 x 2 = 4 × d × ( d + x + 2 0 ) 3 x 2 = 4 × 2 2 0 − x × ( 2 2 0 − x + 2 x + 4 0 ) = ( 2 0 − x ) ( 6 0 + x ) ⟹ 4 x 2 + 4 0 x − 1 2 0 0 = 0 ⟹ x 2 + 1 0 − 3 0 0 = 0 ⟹ x = − 5 + 5 1 3
The area of the rectangle
= 3 x 2 = 3 [ 5 ( 1 3 − 1 ) ] 2 ≈ 2 9 4
Let the top left corner of the rectangle be C , the segment A B intersect the left edge and right edge of the rectangle at D and E respectively. Due to symmetry, we note that A D = B E = d = 2 A B − D E = 2 2 0 − x . And B D = B E + D E = 2 2 0 − x + x = 2 2 0 + x . By Pythagorean theorem ,
B D 2 + C D 2 ( 2 2 0 + x ) 2 + ( 2 3 x ) 2 4 x 2 + 4 0 x + 4 0 0 + 4 3 x 2 x 2 + 1 0 x + 1 0 0 x 2 + 1 0 x + 2 5 ( x + 5 ) 2 x + 5 ⟹ x = B C 2 = 2 0 2 = 4 0 0 = 4 0 0 = 3 2 5 = 3 2 5 = 5 1 3 = 5 1 3 − 5
Then the area of the rectangle A = 3 x ⋅ x = 3 ( 5 1 3 − 5 ) 2 ≈ 2 9 3 . 9 6 7 8 8 2 7 2 9 ≈ 2 9 4 .