Inscribed Bonanza 2

Level pending

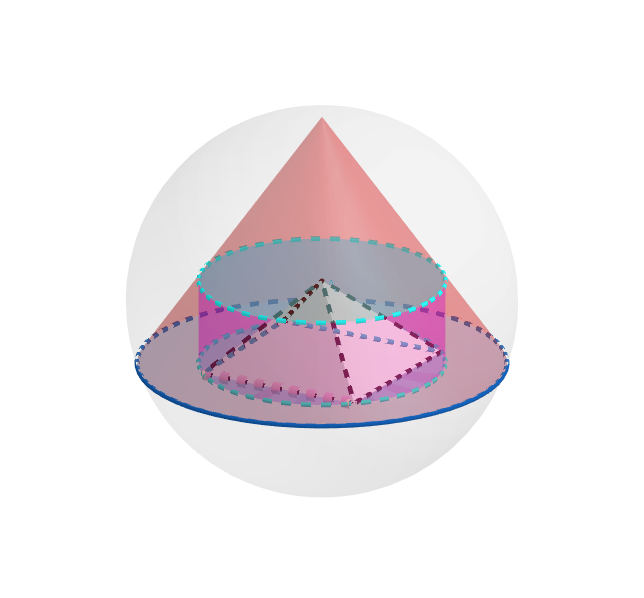
For each positive integer n n :

Let V s ( n ) , V p ( n ) , V c ( n ) V_{s}(n), V_{p}(n), V_{c}(n) and V m ( n ) V_{m}(n) be the volumes of the sphere, right circular cone, right circular cylinder and square pyramid respectively so that:

V p ( n ) V_{p}(n) is the volume of the largest right circular cone inscribed in the sphere of volume V s ( n ) V_{s}(n)

V c ( n ) V_{c}(n) is the volume of the largest right circular cylinder inscribed in the right circular cone of volume V p ( n ) V_{p}(n)

V m ( n ) V_{m}(n) is the volume of the largest square pyramid inscribed in the right circular cylinder of volume V c ( n ) V_{c}(n) .

and

V s ( n + 1 ) V_{s}(n + 1) is the volume of the largest sphere inscribed in the square pyramid of volume V m ( n ) V_{m}(n) .

If V p ∗ V c ∗ V m V s 3 = 1 π ( a b ) a ∗ c ( b a ∗ b ∗ α b b a ∗ b ∗ α b − a b ) b \dfrac{V_{p} * V_{c} * V_{m}}{V_{s}^3} = \dfrac{1}{\pi}(\dfrac{a}{b})^{a * c}(\dfrac{b^{a * b} * \alpha^{b}}{b^{a * b} * \alpha^{b} - a^{b}})^b , where α = 1 + 2 2 \alpha = \dfrac{1 + \sqrt{2}}{2} and a , b a,b and c c are distinct primes, find a + b + c a + b + c .


The answer is 12.

Rocco Dalto by Rocco Dalto , 67, USA

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

1 solution

Rocco Dalto
Jan 28, 2019

Let V s ( 1 ) = 4 3 π R 3 , V p ( 1 ) = 1 3 π r 2 H , V c ( 1 ) = π x 2 h V_{s}(1) = \dfrac{4}{3}\pi R^3, \:\ V_{p}(1) = \dfrac{1}{3}\pi r^2 H, \:\ V_{c}(1) = \pi x^2 h and V m ( 1 ) = 1 3 y 2 h V_{m}(1) = \dfrac{1}{3}y^2 h .

For the diagrams use R = R 1 , r = r 1 , H = H 1 x = x 1 h = h 1 R = R_{1}, \:\ r = r_{1}, H = H_{1} \:\ x = x_{1} h = h_{1} and y = y 1 y = y_{1}

R 1 2 = ( H 1 − r 1 ) 2 + r 2 = H 1 2 − 2 H 1 R 1 + R 1 2 + r 1 2 ⟹ r 1 2 = 2 H 1 R 1 − H 1 2 ⟹ V p ( 1 ) = 1 3 π ( 2 H 1 2 R 1 − H 1 3 ) ⟹ R_{1}^2 = (H_{1} - r_{1})^2 + r^2 = H_{1}^2 - 2H_{1}R_{1} + R_{1}^2 + r_{1}^2 \implies r_{1}^2 = 2H_{1}R_{1} - H_{1}^2 \implies V_{p}(1) = \dfrac{1}{3}\pi(2H_{1}^2R_{1} - H_{1}^3) \implies

d V p ( 1 ) d H 1 = π 3 R 1 H 1 ( 4 R 1 − 3 H 1 ) = 0 H 1 ≠ 0 ⟹ H 1 = 4 3 R 1 ⟹ r 1 = 2 2 3 R 1 ⟹ V p ( 1 ) = ( 2 3 ) 3 V s ( 1 ) \dfrac{dV_{p}(1)}{dH_{1}} = \dfrac{\pi}{3}R_{1}H_{1}(4R_{1} - 3H_{1}) = 0 \:\ H_{1} \neq 0 \implies H_{1} = \dfrac{4}{3}R_{1} \implies r_{1} = \dfrac{2\sqrt{2}}{3}R_{1} \implies \boxed{V_{p}(1) = (\dfrac{2}{3})^3 V_{s}(1)}

The two triangles in the above diagram are similar ⟹ r 1 − x 1 r 1 = h 1 H 1 ⟹ h 1 = ( r 1 − x 1 ) H 1 r 1 ⟹ V c ( 1 ) = π H 1 r 1 ( r 1 x 1 2 − x 1 3 ) ⟹ d V c ( 1 ) d x 1 = π H 1 x 1 r 1 ( 2 r 1 − 3 x 1 ) = 0 \implies \dfrac{r_{1} - x_{1}}{r_{1}} = \dfrac{h_{1}}{H_{1}} \implies h_{1} = \dfrac{(r_{1} - x_{1})H_{1}}{r_{1}} \implies V_{c}(1) = \dfrac{\pi H_{1}}{r_{1}}(r_{1}x_{1}^2 - x_{1}^3) \implies \dfrac{dV_{c}(1)}{dx_{1}} = \dfrac{\pi H_{1}x_{1}}{r_{1}}(2r_{1} - 3x_{1}) = 0 x 1 ≠ 0 ⟹ x 1 = 2 3 r 1 ⟹ h 1 = H 1 3 x_{1} \neq 0 \implies x_{1} = \dfrac{2}{3}r_{1} \implies h_{1} = \dfrac{H_{1}}{3}

r 1 = 2 2 3 R 1 r_{1} = \dfrac{2\sqrt{2}}{3}R_{1} and H 1 = 4 3 R 1 ⟹ x 1 = 4 2 9 R 1 H_{1} = \dfrac{4}{3}R_{1} \implies x_{1} = \dfrac{4\sqrt{2}}{9}R_{1} and h 1 = 4 9 R 1 ⟹ V c ( 1 ) = ( 2 3 ) 5 V s ( 1 ) h_{1} = \dfrac{4}{9}R_{1} \implies \boxed{V_{c}(1) = (\dfrac{2}{3})^5V_{s}(1)}

y 1 = 2 x 1 y_{1} = \sqrt{2}x_{1} and x 1 = 4 2 9 R 1 ⟹ y 1 = 8 9 R 1 ⟹ V m ( 1 ) = 1 π ( 2 3 ) 6 V s ( 1 ) x_{1} = \dfrac{4\sqrt{2}}{9}R_{1} \implies y_{1} = \dfrac{8}{9}R_{1} \implies \boxed{V_{m}(1) = \dfrac{1}{\pi}(\dfrac{2}{3})^6 V_{s}(1)}

From above y 1 = 8 9 R 1 y_{1} = \dfrac{8}{9}R_{1} and h 1 = 4 9 R 1 h_{1} = \dfrac{4}{9}R_{1}

⟹ \implies the slant height s = y 1 2 + 4 h 1 2 2 = 4 2 9 R 1 s = \dfrac{\sqrt{y_{1}^2 + 4h_{1}^2}}{2} = \dfrac{4\sqrt{2}}{9}R_{1}

and the area of the above triangle is A = 1 2 y 1 h 1 = ( y 1 + 2 s 2 ) R 2 ⟹ R 2 = y 1 h 1 y 1 + 2 s = 4 9 ( 1 + 2 ) R 1 A = \dfrac{1}{2}y_{1}h_{1} = (\dfrac{y_{1} + 2s}{2})R_{2} \implies R_{2} = \dfrac{y_{1}h_{1}}{y_{1} + 2s} = \dfrac{4}{9(1 + \sqrt{2})}R_{1}

Let α = 1 + 2 2 ⟹ R 2 = 2 9 α R 1 \alpha = \dfrac{1 + \sqrt{2}}{2} \implies R_{2} = \dfrac{2}{9\alpha}R_{1} .

In General:

For n ≥ 2 n \geq 2 :

R n = ( 2 9 α ) R n − 1 = ( 2 9 α ) n − 1 R 1 R_{n} = (\dfrac{2}{9\alpha})R_{n - 1} = (\dfrac{2}{9\alpha})^{n - 1}R_{1}

⟹ \implies

( r n , H n ) = ( 2 2 3 ( 2 9 α ) n − 1 R 1 , 4 3 ( 2 9 α ) n − 1 R 1 ) (r_{n},H_{n}) = (\dfrac{2\sqrt{2}}{3}(\dfrac{2}{9\alpha})^{n - 1}R_{1} ,\:\ \dfrac{4}{3} (\dfrac{2}{9\alpha})^{n - 1}R_{1})

( x n , h n ) = ( 4 2 9 ( 2 9 α ) n − 1 R 1 , 4 9 ( 2 9 α ) n − 1 R 1 ) (x_{n},h_{n}) = (\dfrac{4\sqrt{2}}{9}(\dfrac{2}{9\alpha})^{n - 1}R_{1} , \:\ \dfrac{4}{9} (\dfrac{2}{9\alpha})^{n - 1}R_{1})

( y n , h n ) = ( 8 9 ( 2 9 α ) n − 1 R 1 , 4 9 ( 2 9 α ) n − 1 R 1 ) (y_{n},h_{n}) = (\dfrac{8}{9}(\dfrac{2}{9\alpha})^{n - 1}R_{1}, \:\ \dfrac{4}{9} (\dfrac{2}{9\alpha})^{n - 1}R_{1})

⟹ \implies

V s ( n ) = ( 8 729 α 3 ) n − 1 V s ( 1 ) V_{s}(n) = (\dfrac{8}{729\alpha^3})^{n - 1}V_{s}(1)

V p ( n ) = ( 2 3 ) 3 ( 8 729 α 3 ) n − 1 V s ( 1 ) V_{p}(n) = (\dfrac{2}{3})^3 (\dfrac{8}{729\alpha^3})^{n - 1}V_{s}(1)

V c ( n ) = ( 2 3 ) 5 ( 8 729 α 3 ) n − 1 V s ( 1 ) V_{c}(n) = (\dfrac{2}{3})^5 (\dfrac{8}{729\alpha^3})^{n - 1}V_{s}(1)

V m ( n ) = 1 π ( 2 3 ) 6 ( 8 729 α 3 ) n − 1 V s ( 1 ) V_{m}(n) = \dfrac{1}{\pi}(\dfrac{2}{3})^6 (\dfrac{8}{729\alpha^3})^{n - 1}V_{s}(1)

⟹ \implies

V s = ( 729 α 3 729 α 3 − 8 ) V s ( 1 ) V_{s} = (\dfrac{729\alpha^3}{729\alpha^3 - 8})V_{s}(1)

V p = ( 2 3 ) 3 ( 729 α 3 729 α 3 − 8 ) V s ( 1 ) V_{p} = (\dfrac{2}{3})^3 (\dfrac{729\alpha^3}{729\alpha^3 - 8})V_{s}(1)

V c = ( 2 3 ) 5 ( 729 α 3 729 α 3 − 8 ) V s ( 1 ) V_{c} = (\dfrac{2}{3})^5 (\dfrac{729\alpha^3}{729\alpha^3 - 8})V_{s}(1)

V m = 1 π ( 2 3 ) 6 ( 729 α 3 729 α 3 − 8 ) V s ( 1 ) V_{m} = \dfrac{1}{\pi}(\dfrac{2}{3})^6 (\dfrac{729\alpha^3}{729\alpha^3 - 8})V_{s}(1)

⟹ V p ∗ V c ∗ V m V s 3 = \implies \dfrac{V_{p} * V_{c} * V_{m}}{V_{s}^3} = 1 π ( 2 3 ) 14 ( 729 α 3 729 α 3 − 8 ) 3 = 1 π ( 2 3 ) 2 ∗ 7 ( 3 2 ∗ 3 α 3 3 2 ∗ 3 α 3 − 2 3 ) 3 = 1 π ( a b ) a ∗ c ( b a ∗ b ∗ α b b a ∗ b ∗ α b − a b ) b ⟹ a + b + c = 12 \dfrac{1}{\pi}(\dfrac{2}{3})^{14}(\dfrac{729\alpha^3}{729\alpha^3 - 8})^3 = \dfrac{1}{\pi}(\dfrac{2}{3})^{2 * 7}(\dfrac{3^{2 * 3}\alpha^3}{3^{2 * 3}\alpha^{3} - 2^{3}})^3 = \dfrac{1}{\pi}(\dfrac{a}{b})^{a * c}(\dfrac{b^{a * b} * \alpha^{b}}{b^{a * b} * \alpha^{b} - a^{b}})^b \implies a + b + c = \boxed{12}

0 Helpful 0 Interesting 0 Brilliant 0 Confused

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...