Inscribed Circles
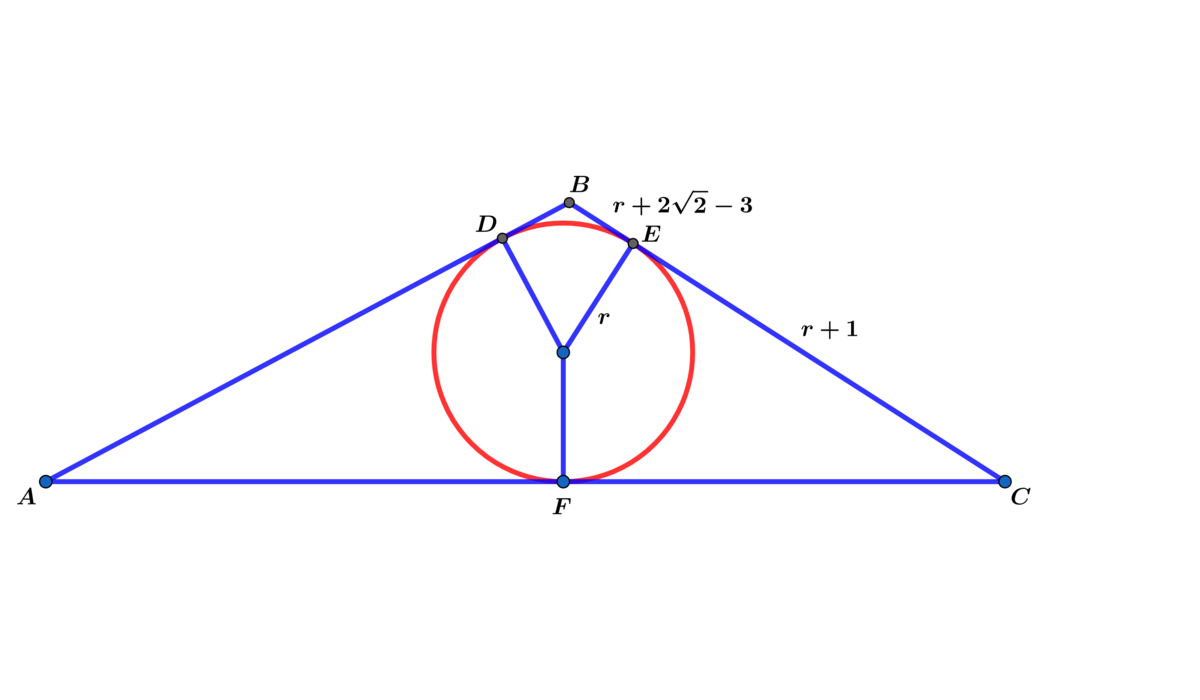
In △ A B C , the inscribed circle with radius r is tangent to A B , B C and A C at points D , E and F respectively.
Folding the arc of the semi-circle at a right angle, as shown below, the radius of the semicircle becomes the height of the tetrahedron.

If A △ A B C = 2 r ( 2 r + 2 ( 2 − 1 ) ) and the volume V T of the tetrahedron can be expressed as V T = β α β ( α − 1 ) β , where α and β are coprime positive integers, find α + β .
The answer is 5.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
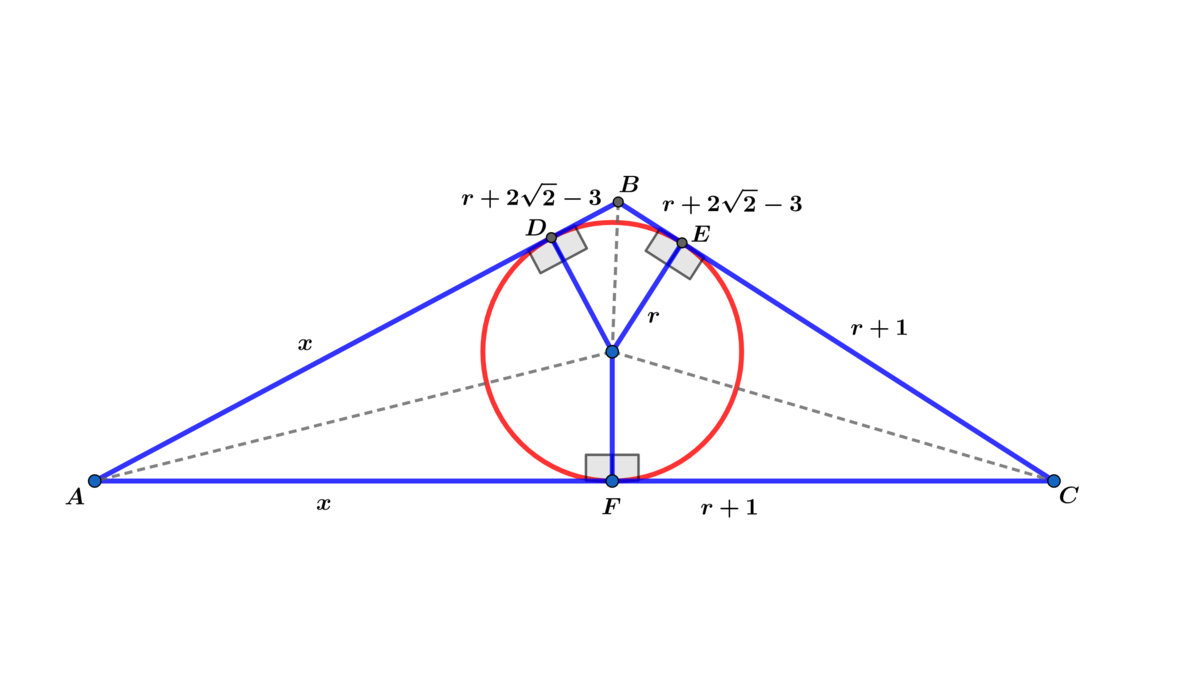
I actually did the problem in general to obtain r = 2 − 1 , so I will present the way I actually did it.
Let a = 2 2 − 3 and b = 1 .
A △ A B C = 2 1 ( 2 x + 4 r + 2 ( a + b ) ) = ( x + 2 r + a + b ) r
Using Heron's formula with s = x + 2 r + a + b ⟹
A △ A B C = ( x + 2 r + a + b ) ( r + a ) ( r + b ) x ⟹
( x + 2 r + a + b ) 2 r 2 = ( x + 2 r + a + b ) ( r + a ) ( r + b ) x ⟹
r 2 x = ( 2 r + a + b ) r 2 = ( r 2 + ( a + b ) r + a b ) x ⟹
( ( a + b ) r + a b ) x = ( 2 r + a + b ) r 2 ⟹ x = ( a + b ) r + a b ( 2 r + a + b ) r 2
⟹ A △ A B C = ( 2 r + a + b ) ( ( a + b ) r + a b r 2 + 1 ) r =
( a + b ) r + a b ( 2 r + a + b ) ( r 2 + ( a + b ) r + a b ) r = 2 ( 2 r + a + b ) r ⟹
r 2 + ( a + b ) r + a b = 2 ( a + b ) r + 2 a b ⟹ r 2 − ( a + b ) r − a b = 0
Letting a = 2 2 − 3 and b = 1 ⟹ r 2 − 2 ( 2 − 1 ) r − ( 2 2 − 3 ) = 0 ⟹ r = 2 − 1 ⟹
A △ A B C = 3 − 2 2 8 ( 2 − 1 ) 4 = 8 ( 2 − 1 ) 2 ⟹
3 8 ( 2 − 1 ) 3 = 3 2 3 ( 2 − 1 ) 3 = β α β ( α − 1 ) β ⟹ α + β = 5 .
Let the center of the inscribed circle be I and let θ = ∠ I C F = ∠ I C E . Then from △ I C E , I C = ( r + 1 ) 2 + r 2 = 2 r 2 + 2 r + 1 , cos θ = 2 r 2 + 2 r + 1 r + 1 , sin θ = 2 r 2 + 2 r + 1 r , and cos 2 θ = cos 2 θ − sin 2 θ = 2 r 2 + 2 r + 1 ( r + 1 ) 2 − r 2 = 2 r 2 + 2 r + 1 2 r + 1 .
As tangents from the same point, C F = C E = r + 1 , B D = B E = r + 2 2 − 3 , and x = A F = A D . Therefore, the perimeter of △ A B C is P = 2 ( r + 1 ) + 2 ( r + 2 2 − 3 ) + 2 x , and the semiperimeter is s = 2 r + 2 2 − 2 + x .
Since A △ A B C = 2 r ( 2 r + 2 ( 2 − 1 ) ) and A △ A B C = r s = r ( 2 r + 2 2 − 2 + x ) , these equations combine and solve to x = 2 r + 2 2 − 2 .
The sides of △ A B C are then A B = 2 r + 2 2 − 2 + r + 2 2 − 3 = 3 r + 4 2 − 5 , A C = 2 r + 2 2 − 2 + r + 1 = 3 r + 2 2 − 1 , and B C = r + 2 2 − 3 + r + 1 = 2 r + 2 2 − 2 .
Then by the law of cosines on △ A B C , cos 2 θ = 2 ( 3 r + 2 2 − 1 ) ( 2 r + 2 2 − 2 ) ( 3 r + 2 2 − 1 ) 2 + ( 2 r + 2 2 − 2 ) 2 − ( 3 r + 4 2 − 5 ) 2 = 3 r + 2 2 − 1 r − 2 2 + 5 .
That means cos 2 θ = 2 r 2 + 2 r + 1 2 r + 1 = 3 r + 2 2 − 1 r − 2 2 + 5 , which rearranges to ( r − 1 ) ( r + 2 − 1 ) 2 = 0 and solves to r = 2 − 1 for r > 0 .
Therefore, V T = 3 1 ⋅ A △ A B C ⋅ r = 3 1 ⋅ 2 r ( 2 r + 2 ( 2 − 1 ) ) ⋅ r = 3 2 3 ( 2 − 1 ) 3 , so α = 2 , β = 3 , and α + β = 5 .