Inscribed circles in a unit circle
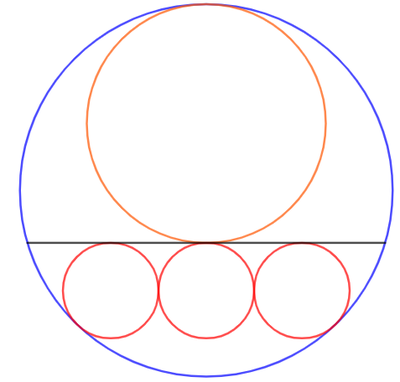
Four circles are inscribed in the blue unit circle. The orange circle has a radius that is times the radius of one of the three congruent red circles. The radius of a red circle is for coprime positive integers and , find .
The answer is 49.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Let the radius of the red circles be r . Then the radius of the orange circle is 2 5 r . Let the tangent points between the blue and orange circle, the orange and the middle red circle, and the blue and the right red circle be R , S , and T respectively. By Pythagorean theorem , we have:
O P 2 ⟹ O P = O Q 2 − P Q 2 = ( O T − Q T ) 2 − P Q 2 = ( 1 − r ) 2 − ( 2 r ) 2 = 1 − 2 r − 3 r 2 = 1 − 2 r − 3 r 2
Now note that:
R S R O + O P − P S 1 + 1 − 2 r − 3 r 2 − r 1 − 2 r − 3 r 2 1 − 2 r − 3 r 2 3 9 r 2 − 1 0 r ⟹ r = 2 × 2 5 r = 5 r = 5 r = 6 r − 1 = 3 6 r 2 − 1 2 r + 1 = 0 = 3 9 1 0 Squaring both sides Since r > 0
Therefore p + q = 1 0 + 3 9 = 4 9 .