Inscribed Ellipse in a Parallelogram
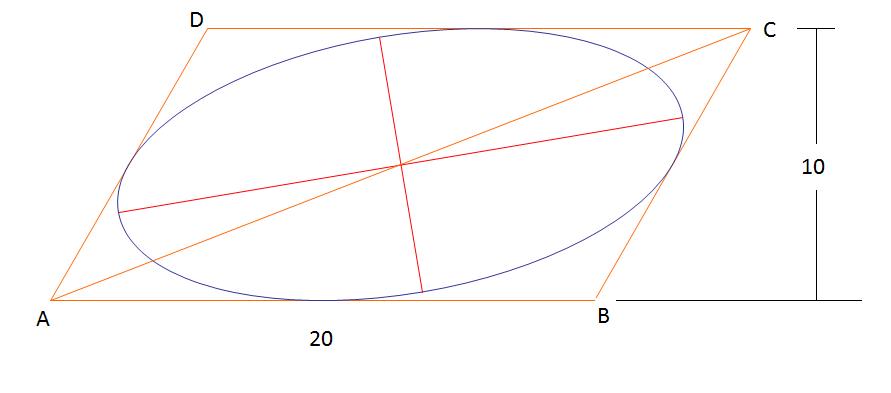
Parallelogram has and an altitude of , and . The ellipse shown is the unique ellipse that is inscribed in the parallelogram and tangent to the midpoints of its four sides. Find the sum of the lengths of the major and minor axes and the angle (in degrees) that the major axis makes with .
That is, enter as your answer , where is the length of the semi-major axis, is the length of the semi-minor axis, and is the angle between the major axis and .
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
We'll look at the given figure as a transformation of the unit square and the inscribed circle within it.
So we start with a square with vertices (0,0), (1,0), (0, 1), (1, 1).
And we find the transformation matrix P , such that a point v is mapped into
P v .
P = [ a c b d ]
Note that with this, ( 0 , 0 ) is automatically mapped into ( 0 , 0 )
The point ( 1 , 0 ) is mapped into ( 2 0 , 0 ) , therefore,
a = 2 0 , c = 0
The point ( 0 , 1 ) is mapped into ( 1 0 / t a n ( π / 3 ) , 1 0 ) , therefore,
b = 1 0 / t a n ( π / 3 ) , d = 1 0
Hence,
P = ⎣ ⎡ 2 0 0 t a n ( π / 3 ) 1 0 1 0 ⎦ ⎤
Now the equation of the original circle (before transformation) is
( r − r c ) T ( r − r c ) = ( 1 / 2 ) 2
where r c = ( 0 . 5 , 0 . 5 )
Let r ′ = P r , then
( P − 1 r ′ − r c ) T ( P − 1 r ′ − r c ) = 4 1
Define r c ′ = P r c , then
( r ′ − r c ′ ) T ( 4 P − T P − 1 ) ( r ′ − r c ′ ) = 1
Let the matrix G = ( 4 P − T P − 1 ) then G is symmetric, and we can diagnonalize, by finding an orthogonal matrix (of eigenvectors) R and a diagonal matrix D such that,
R T G R = D
Note that R can be written as
R = [ cos θ sin θ − sin θ cos θ ]
where θ will be specified below.
Based on this, we can introduce a new vector w and define it by
r ′ − r c ′ = R w
This leades to
w T D w = 1
Which is the equation of an ellispe centered at the origin (of the w − coordinate frame) In terms of r ′ , this is an ellipse centered at r c ′ , with tilted axes which make an angle of θ with the X and Y axes. The lengths of the semi-major and semi-minor axes of the ellipse are equal to the reciprocal of the square root of the diagonal entries of the diagonal matrix D . So the whole problem reduces to finding the eigenstructure of matrix G. The formula for calculating R and D is a follows:
θ = 2 1 tan − 1 g 1 1 − g 2 2 2 g 1 2
Thus R is now fully determined. The diagonal elements of D are as follows
d 1 1 = g 1 1 cos 2 θ + g 2 2 sin 2 θ + 2 g 1 2 sin 2 θ
d 2 2 = g 2 2 cos 2 θ + g 1 1 sin 2 θ − 2 g 1 2 sin 2 θ
This completely specifies the diagonalization of matrix G .
Performing the calculations gives
θ = 9 . 5 5 3 3 ∘
a = 1 0 . 5 2 4 4
b = 4 . 7 5 0 9
The angle that A C makes with the horizontal is 2 1 . 2 0 6 0 ∘
This makes the answer
2 ( 1 0 . 5 2 4 4 ) + 2 ( 4 . 7 5 0 9 ) + ( 2 1 . 2 0 6 0 − 9 . 5 5 3 3 ) = 4 2 . 2 0 .