Inscribed ellipse in a pentagon
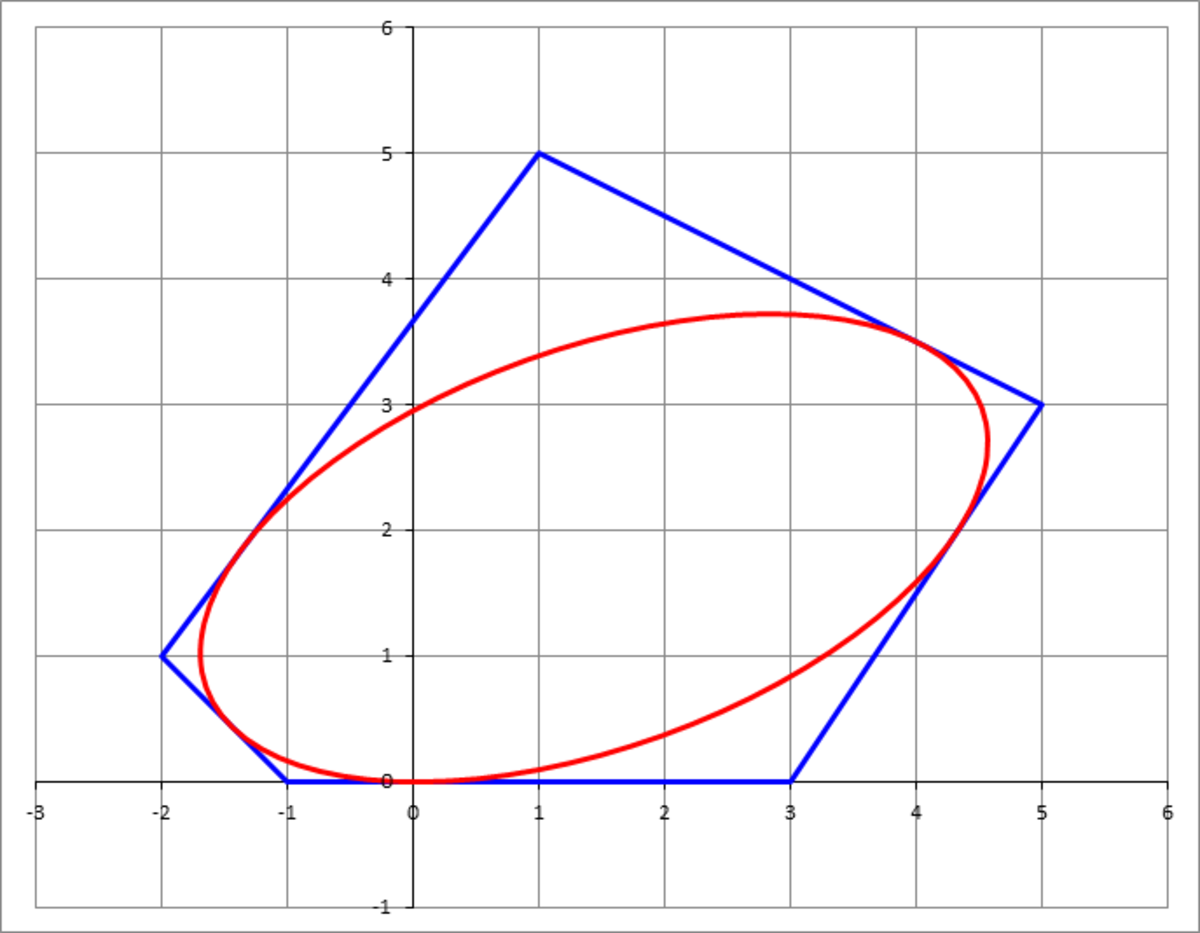
An irregular pentagon is specified by its vertices: . A unique ellipse can be inscribed within this pentagon. If is the sum of its semi-major and semi-minor axes lengths, then submit .
The answer is 486.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
The idea of the solution is described here .
Python was used to find a solution.
The semi-major and semi-minor axes of the ellipse are equal
M = 2 5 0 2 4 0 0 0 4 1 4 9 5 8 0 7 3 6 9 2 1 6 0 0 − 1 2 5 2 4 0 1 1 5 2 0 0 4 2 2 1 4 7 6 8 9
m = 2 5 0 2 4 0 0 0 1 2 5 2 4 0 1 1 5 2 0 0 4 2 2 1 4 7 6 8 9 + 4 1 4 9 5 8 0 7 3 6 9 2 1 6 0 0
t r u n c ( 1 0 0 ( M + m ) ) = 4 8 6