Inscribed Ellipse in a Rhombus
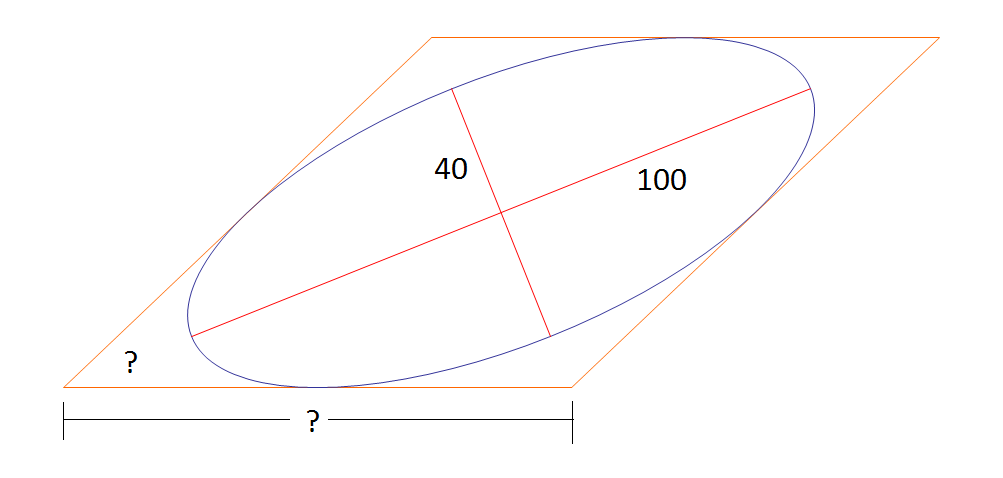
An ellipse is inscribed inside a rhombus (a parallelogram with equal sides). The ellipse is tangent to the rhombus at the midpoints of the four sides. Given that the semi-major axis of the ellipse is 1 0 0 units and the semi-minor axis is of length 4 0 units, then if the side length of the rhombus is A and the acute angle of the rhombus is θ (measured in degrees), enter the value of A + θ correct to two decimal places.
The answer is 195.92.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
The given rhombus can be thought of as being a transformed figure from a square. Consider the unit square with vertices (0,0), (1,0), (0,1) and (1,1). (See figure below, left). Consider the circle centered at the center of the square with diameter 1. Also, consider the circle centered at the center of the square and passes through the four vertices. Obviously the diameter of the outer circle is 2 . Now transforming all three shapes (the square , the inner circle, the outer circle) gives the figure on the right.
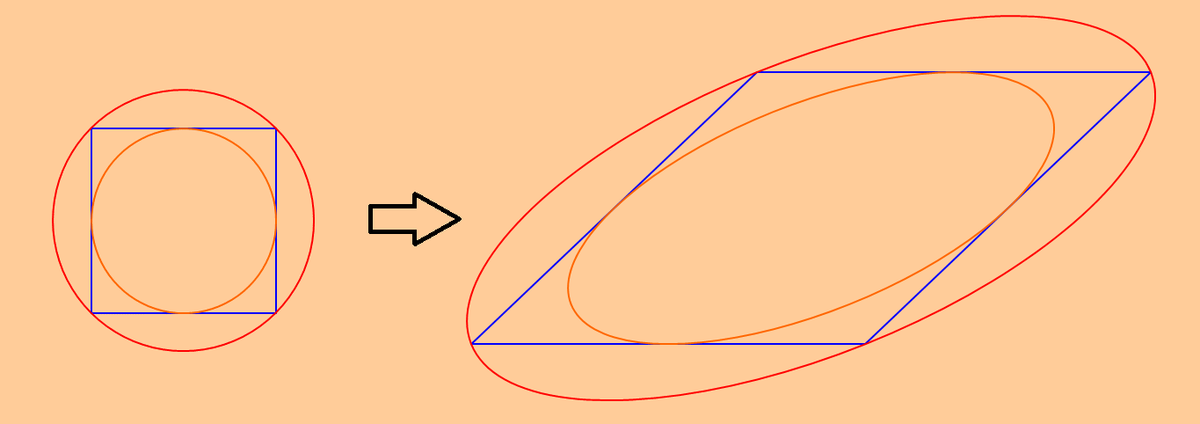
Since the radius of the outer circle is
2
times the radius of the inner circle, it follows that semi-minor axis of the outer ellipse is
2
times the semi-minor axis of the inner ellipse. Similarly the semi-major axis of the outer ellipse is
2
times the semi-major axis of the inner ellipse.
But the minor and major axes of the outer ellipse coincide with the small and large diameters of the rhombus. This follows from the symmetry of the figure, and the fact that the two diameters of the rhombus are perpendicular to each other .
Hence, the small semi-diameter of the rhombus is
4
0
2
, and the large semi-diameter of the rhombus is
1
0
0
2
.
Hence, the side length is
2
1
0
0
2
+
4
0
2
=
1
5
2
.
3
1
6
and half of the small angle is
tan
−
1
(
4
0
/
1
0
0
)
=
tan
−
1
(
2
/
5
)
=
2
1
.
8
∘
. Therefore, the answer is
1
5
2
.
3
1
6
+
2
(
2
1
.
8
)
=
1
9
5
.
9
2
This can be done by non-uniform scaling. Consider a circle of radius OA = OB = 100 and an inscribing square PQRS of side 200 and half diagonal O P = O Q = 2 2 0 0 Scale both in the Y direction by a factor 1 0 0 4 0 = 5 2 So the radius OB becomes OB' (the semi-major axis) and OP becomes OP' (semi diagonal of square to parallelogram).
Scaling does not change the ratio (1:1) in which the points of tangency divide the sides of the squares. So they still remain the midpoints of the parallelogram that we now have.
So OA and OQ remain the same while OP and OB shrink by the same factor. So tan P ′ Q O = O Q O P ′ = O A O B ′ = 1 0 0 4 0 Giving angle P ′ Q O = 2 arctan 5 2 = 2 × 2 1 . 8 ° = 43.6°
Side of parallelogram P ′ Q = cos 2 1 . 8 ° 2 2 0 0 = 152.32
So the required quantity is 1 5 2 . 3 1 + 4 3 . 6 = 195.92