Inscribed Ellipse
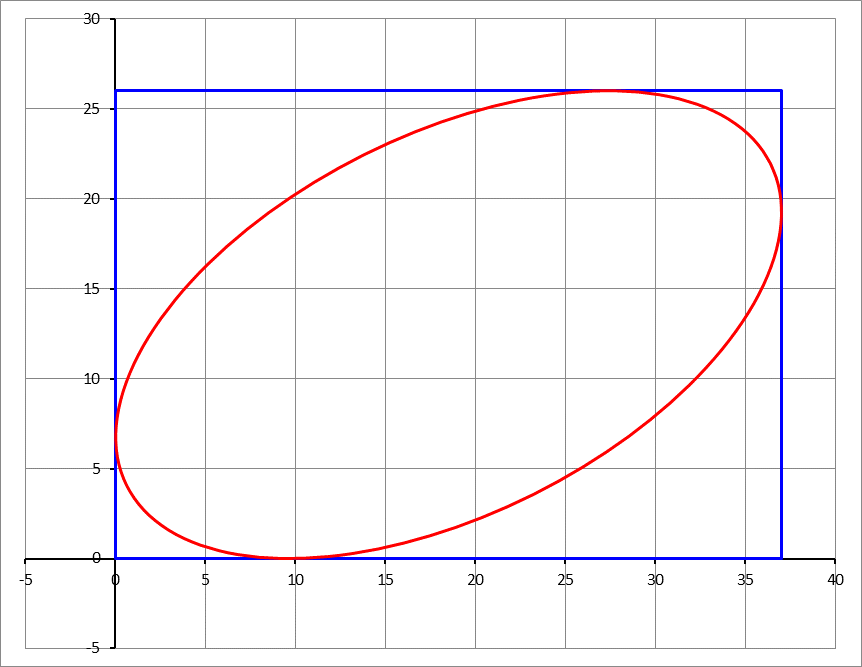
A rectangle measures 3 7 × 2 6 with the longer side extending along the x -axis. You want to inscribe an ellipse in the rectangle, such that its major axis makes an angle θ = 2 1 cos − 1 ( 5 3 ) with the positive x -axis, as shown in the attached figure. Find the length of the semi-major axis. The figure is drawn to scale.
The answer is 20.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
Let A = 3 7 , B = 2 6 , then from symmetry, the center of the ellipse is at r C = ( A / 2 , B / 2 ) . The equation of the ellipse is,
( r − r C ) T R D R T ( r − r C ) = 1
where R is the rotation matrix, given by,
R = R ( θ ) = [ cos θ sin θ − sin θ cos θ ]
and D = diag { 1 / a 2 , 1 / b 2 } with a , b being the semi-major and semi-minor axes lengths.
The gradient (the normal to the curve) is
∇ = 2 R D R T ( r − r C )
At the right tangency point r 1 , the gradient is a positive multiple of i (the unit vector along the positive x-axis), hence
R D R T ( r 1 − r C ) = α i
from which,
( r 1 − r C ) = α R D − 1 R T i
Plugging this into the ellipse equation, gives
α = i T R D − 1 R T i 1
Now, the x-component of ( r 1 − r C ) at the tangency point is just 2 A , so
2 A = α i T R D − 1 R T i = i T R D − 1 R T i
A similar equation can be developed for the upper tangency point, namely,
2 B = j T R D − 1 R T j
Now D − 1 = diag { a 2 , b 2 } , so
i T R D − 1 R T i = a 2 cos 2 θ + b 2 sin 2 θ
and
j T R D − 1 R T j = a 2 sin 2 θ + b 2 cos 2 θ
And we end up with the following linear system in a 2 and b 2
Note that since cos 2 θ = 5 3 , then cos 2 θ = 5 4 and sin 2 θ = 5 1 , and hence,
5 4 a 2 + 5 1 b 2 = 4 3 7 2
5 1 a 2 + 5 4 b 2 = 4 2 6 2
from which, and using Cramer's rule,
a 2 = 2 5 1 6 − 2 5 1 2 0 1 ( 4 ( 3 7 ) 2 − ( 2 6 ) 2 ) = 4 0 0 , hence, a = 2 0
Let us consider the standard ellipse a 2 x 2 + b 2 y 2 = 1 , with a > b . Tilting the ellipse about the origin so that the semi-major axis makes an angle θ with the x -axis, the equation becomes a 2 ( x cos θ + y sin θ ) 2 + b 2 ( x sin θ − y cos θ ) 2 = 1 . Shifting the center of the ellipse to ( x c , y c ) , the equation becomes a 2 ( ( x − x c ) cos θ + ( y − y c ) sin θ ) ) 2 + b 2 ( ( x − x c ) sin θ − ( y − y c ) cos θ ) ) 2 = 1 . For θ = 2 1 cos − 1 5 3 = tan − 1 2 1 = sin − 1 5 1 = cos − 1 5 2 and ( x c , y c ) = ( 2 3 7 , 1 3 ) , the equation of the ellipse of this problem is:
a 2 ( 2 x + y − 5 0 ) 2 + b 2 ( x − 2 y + 7 . 5 ) 2 a 2 ( 2 x + y − 5 0 ) ( 2 + d x d y ) + b 2 ( x − 2 y + 7 . 5 ) ( 1 − 2 d x d y ) a 2 ( 2 x + y − 5 0 ) ( 2 d y d x + 1 ) + b 2 ( x − 2 y + 7 . 5 ) ( d y d x − 2 ) = 5 . . . ( 1 ) = 0 . . . ( 2 a ) = 0 . . . ( 2 b ) Differentiate w.r.t. x Differentiate w.r.t. y
Let the point where the ellipse touches the x -axis be ( x 0 , 0 ) . Note that d x d y = 0 at the point. Then
⎩ ⎪ ⎨ ⎪ ⎧ a 2 ( 2 x 0 − 5 0 ) 2 + b 2 ( x 0 + 7 . 5 ) 2 = 5 a 2 2 ( 2 x 0 − 5 0 ) + b 2 x 0 + 7 . 5 = 0 . . . ( 1 a ) . . . ( 2 a a )
( 1 a ) − ( x 0 + 7 . 5 ) ( 2 a a ) : a 2 2 x 0 − 5 0 = − 1 3 1 ⟹ x 0 = 2 6 6 5 0 − a 2
( 2 a a ) : − 1 3 2 + 2 6 b 2 8 4 5 − a 2 = 0 ⟹ b 2 = 4 8 4 5 − a 2 . . . ( 3 a )
Similarly, let the point where the ellipse touches the y -axis be ( 0 , y 0 ) . Note that d y d x = 0 at the point. Then
⎩ ⎪ ⎨ ⎪ ⎧ a 2 ( y 0 − 5 0 ) 2 + b 2 ( 7 . 5 − 2 y 0 ) 2 = 5 a 2 y 0 − 5 0 − b 2 2 ( 7 . 5 − 2 y 0 ) = 0 . . . ( 1 b ) . . . ( 2 b b )
2 ( 1 b ) + ( 7 . 5 − 2 y 0 ) ( 2 b b ) : a 2 y 0 − 5 0 = − 3 7 4 ⟹ y 0 = 3 7 1 8 5 0 − 4 a 2
( 2 b b ) : − 3 7 4 + 3 7 b 2 6 8 4 5 − 1 6 a 2 = 0 ⟹ b 2 = 4 6 8 4 5 − 1 6 a 2 . . . ( 3 b )
From ( 3 a ) = ( 3 b ) : 8 4 5 − a 2 = 6 8 4 5 − 1 6 a 2 ⟹ the semi-major axis a = 2 0 .
Solving this problem (at least, the way I did it) leads to some slightly messy algebra; the key steps are as follow:
The idea is to use the general equation for an ellipse; we'll plug in the info we have, work out the coefficients, and then work out the axes.
The general equation whose coefficients we'll find is A x 2 + B x y + C y 2 + D x + E y + F = 0 .
Firstly, recentre the ellipse at the origin, so that the tangent lines are y = ± 1 3 and x = ± 2 3 7 . This simplifies the equation and makes D = E = 0 , and F = a 2 b 2 , where a , b are the semi-major and semi-minor axes.
Secondly, we have sin θ = 5 1 and cos θ = 5 2 . This (plus the info in the link above) gives the relations
A = 5 a 2 + 5 4 b 2
B = 5 4 ( b 2 − a 2 )
C = 5 4 a 2 + 5 b 2
Plug in y = 1 3 . This gives a quadratic in x . Since this line is a tangent to the ellipse, the quadratic has just one solution; so its discriminant is zero. Working the algebra through and substituting in we get a 2 + 4 b 2 = 8 4 5
Similarly, plugging in x = 2 3 7 , we get 4 a 2 + b 2 = 4 6 8 4 5 .
Solving these gives a 2 = 4 0 0 , or a = 2 0 .