Inscribed Hexagon

Geometry Level 2

An irregular hexagon is inscribed in a circle, and I am interested in finding the measure of one specific interior angle of the hexagon.

If I am not allowed to measure it directly, what is the minimum number of other interior angles that I need to measure?

1 2 3 4 5

2 solutions

Marta Reece
Jul 5, 2017

Line $AB$ divides the hexagon into two cyclic quadrilaterals.

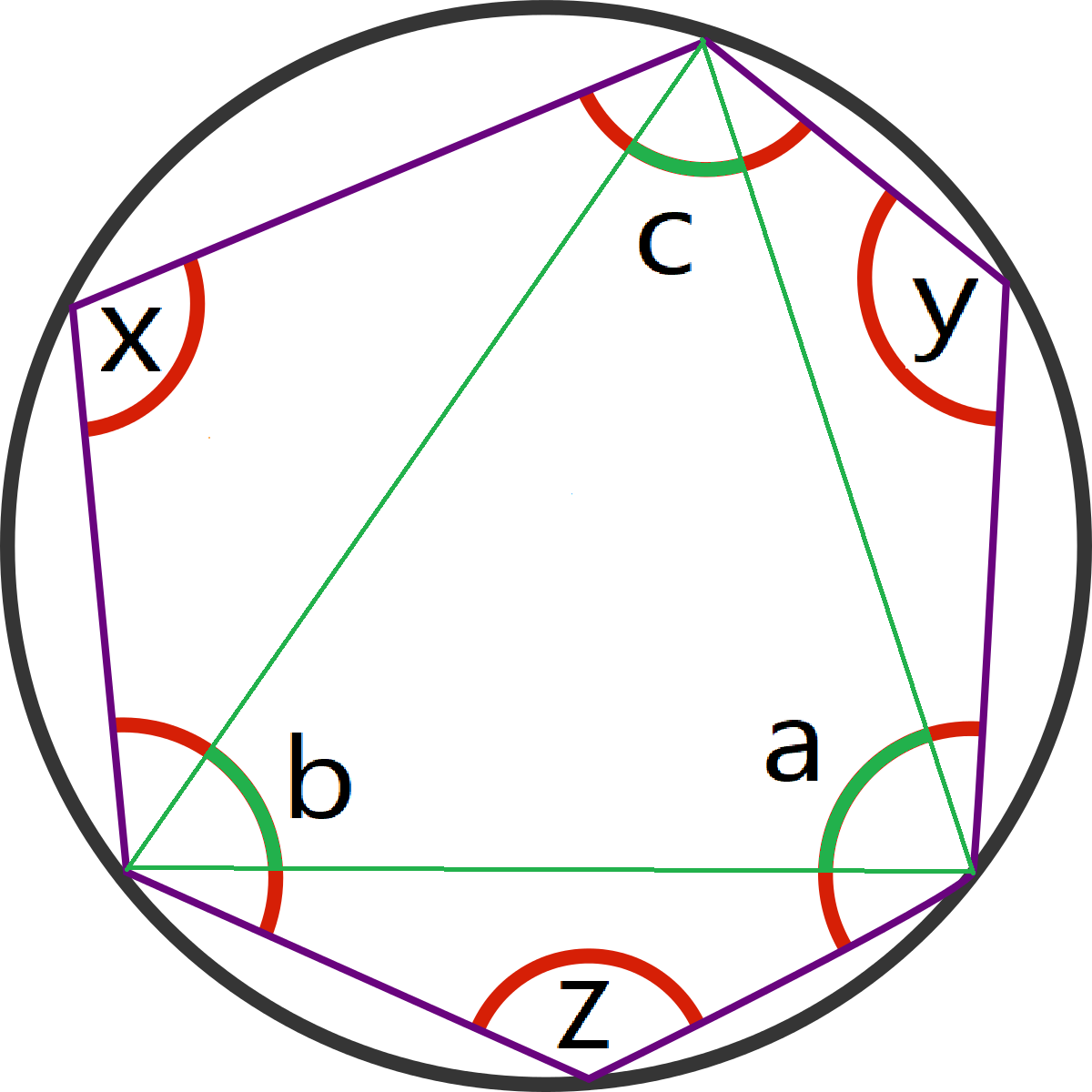
In the top quadrilateral $x_1+b=180^\circ$

In the bottom quadrilateral $x_2+d=180^\circ$

Therefore $x=x_1+x_2=180^\circ-b+180^\circ-d=360^\circ-b-d$

So $x$ can be calculated from just $\boxed2$ other angles.

Why 2 is the minimum?

Áron Bán-Szabó - 3 years, 11 months ago

How do you know that 1 is not achievable?

Pi Han Goh - 3 years, 11 months ago

If I have only one, I can pick at least one other arbitrarily and by doing so get any number of different answers for $x$ .

Marta Reece - 3 years, 11 months ago

旭李
Sep 7, 2018

x+a=180°, y+b=180°, z+c=180°, a+b+c=180°. Then 180°×3-x-y-z=180°, x=360°-y-z. You can measure y and z and then caiculate x.