Inscribed Regular Polygons
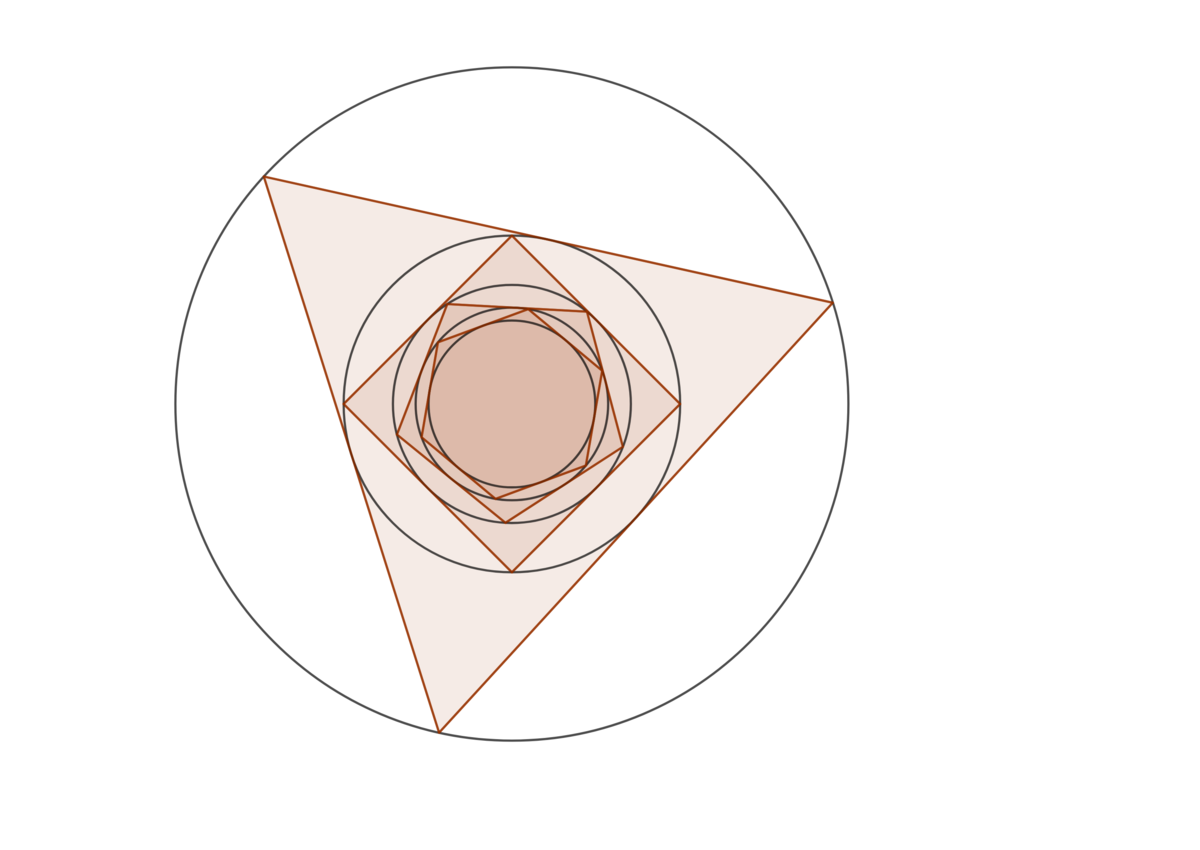
Inscribed in the outer circle is an equilateral triangle, inside it is another circle, inside it is a square, then a circle, then a regular pentagon, then a circle, then a regular hexagon, and finally, another circle is inscribed in the hexagon. What if the ratio of the radius of the smallest circle to that of the largest circle? Find a closed-form of the ratio, x , and submit ⌊ 1 0 5 x ⌋ .
Bonus: If we extend this sequence to infinity, does x converge? If so, to what value?
The answer is 24770.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
The infinite product is a known constant . By the very construction, the infinite product must converge.
The series converges as well. For sufficiently large n , cos n π → 1 − 2 1 ( n π ) 2
And thus ln ( cos n π ) → ln [ 1 − 2 1 ( n π ) 2 ]
And for sufficiently small X > 0 (close to 0), ln ( 1 − X ) → X , so continuing from above,
ln ( cos n π ) → ln [ 1 − 2 1 ( n π ) 2 ] → 2 1 ( n π ) 2
In other words, for sufficiently large n , the series resembles a p -series with p = 2 , so it converges.
The ratio of the inradius, r , to the circumradius, R , of a regular n-gon is
R r = cos n π
So the required ratio of our sequence of four polygons can be expressed becomes
x = cos 3 π ⋅ cos 4 π ⋅ cos 5 π ⋅ cos 6 π = 3 2 6 + 3 0 ≈ 0 . 2 4 7 7 0 9 8
Trigonometry identities courtesy of Wolfram Alpha . And the requested result is 2 4 7 7 0 .
Consider a regular n -sided polygon, then the central angle is n 2 π , the outer radius r o is the circumradius of the polygon and the inner radius r i is the apothem or inradius of the polygon. The ratio r o r i = cos ( n π ) .
Label the radii of the five circles r 1 to r 5 from outermost to innermost. We have r 1 r 2 = cos 3 π , r 2 r 3 = cos 4 π , r 3 r 4 = cos 5 π , and r 4 r 5 = cos 6 π . Then we have:
x ⟹ ⌊ 1 0 5 x ⌋ = r 1 r 5 = cos 3 π cos 4 π cos 5 π cos 6 π = 2 1 ⋅ 2 1 ⋅ 4 1 + 5 ⋅ 2 3 = 1 6 2 3 + 1 5 = 3 2 6 + 3 0 ≈ 0 . 2 4 7 7 0 9 8 5 4 = 2 4 7 7 0
When n → ∞ , x = n = 3 ∏ ∞ cos n π . Since ∑ n = 3 ∞ ln ( cos n π ) ≈ − 2 . 1 6 3 3 3 (according the Wolfram Alpha, the series converges by comparison test -- hope that @Pi Han Goh can prove this), x ≈ e − 2 . 1 6 3 3 3 ≈ 0 . 1 1 4 9 4 2 .