Inscribed Rhombus
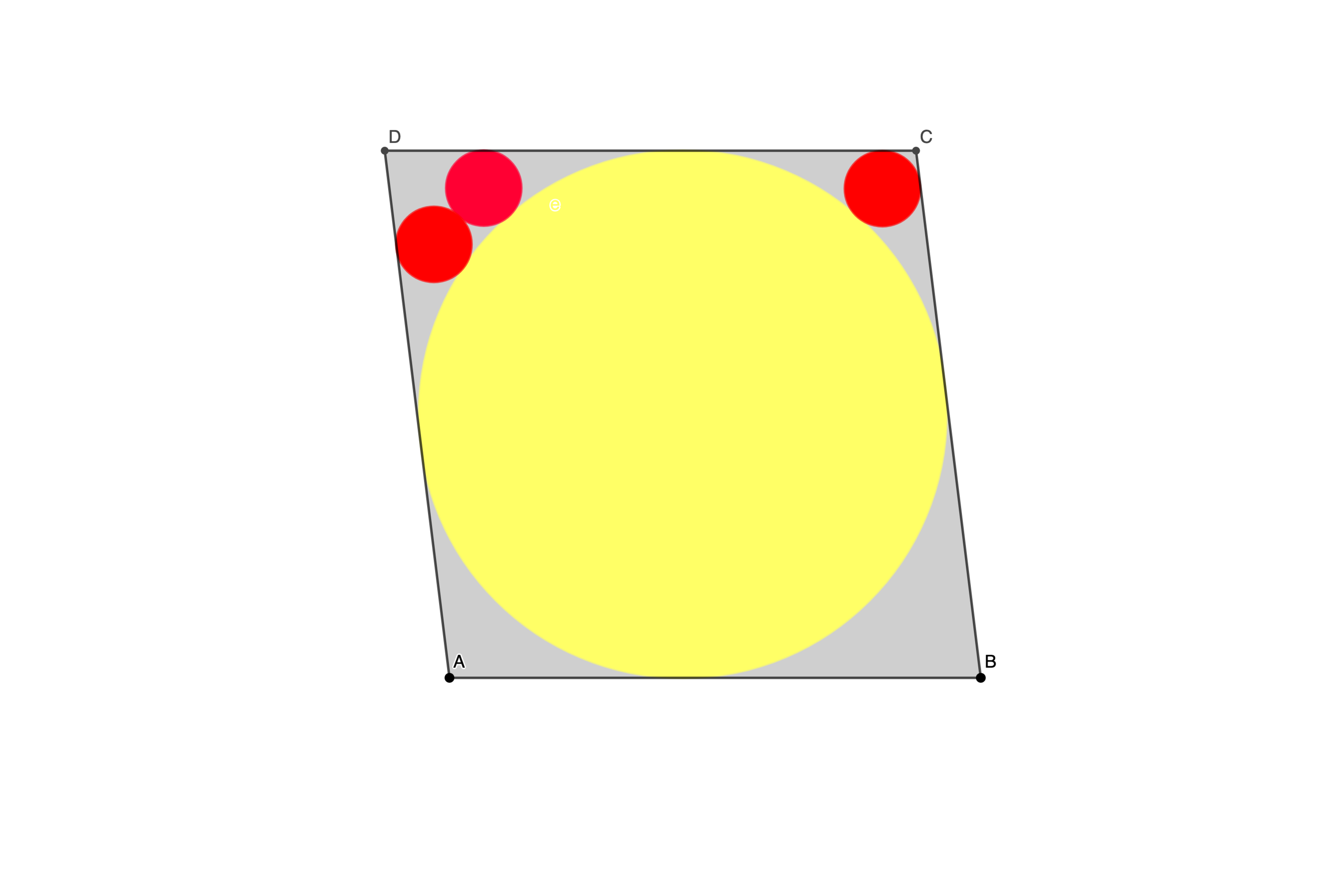
A B C D is a rhombus with four inscribed circles. The red circles are congruent. What is the ratio of the radius of the yellow circle to the radius of a red circle?
The answer is 7.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Nice solution.
Log in to reply
Thank you! Happy New Year!
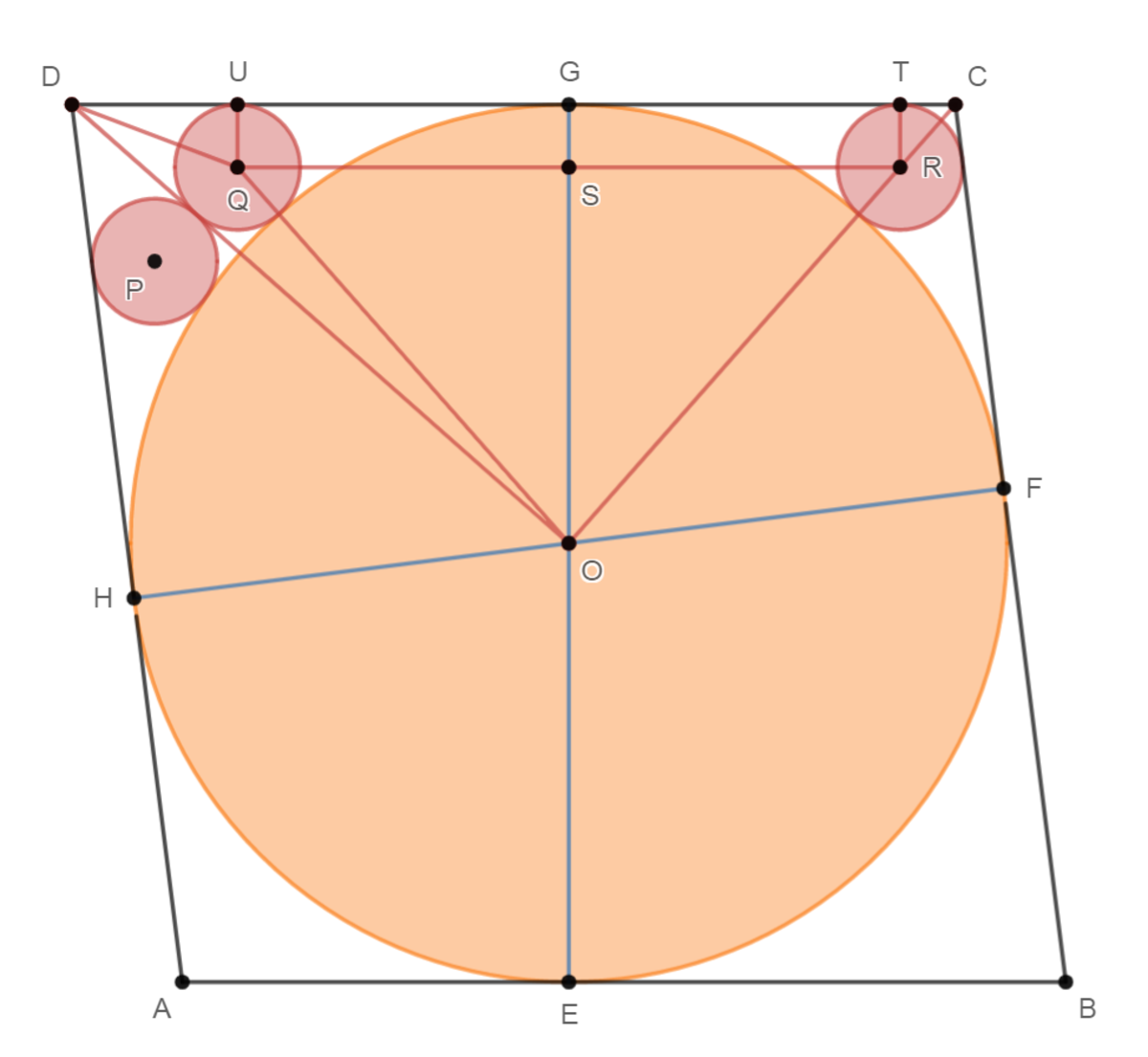
Let radius of the yellow circle be 1 and its center O ; the radius of the red circles be r and their centers be P , Q , and R ; and ∠ D = 4 θ . Then ∠ C = 1 8 0 ∘ − 4 θ . Let E G and F H through O be perpendicular to the sides of the A B C D as shown. Then O E = O F = O G = O H = 1 .
From the figure:
C T + T G T R ⋅ cot 2 C + T G r cot ( 9 0 ∘ − 2 θ ) + S R r tan 2 θ + O R 2 − O S 2 r tan 2 θ + ( 1 + r ) 2 − ( 1 − r ) 2 r tan 2 θ + 2 r r tan 2 θ + 2 r − tan 2 θ ⟹ r ⟹ r = C G = O G ⋅ cot 2 C = 1 ⋅ cot ( 9 0 ∘ − 2 θ ) = tan 2 θ = tan 2 θ = tan 2 θ = 0 = 2 tan 2 θ 4 + 4 tan 2 2 θ − 2 = tan 2 θ sec 2 θ − 1 = sin 2 θ 1 − cos 2 θ = 2 sin θ cos θ 2 sin 2 θ = tan θ B e a u t i f u l !
Similarly,
D U + U G D U + Q S U Q ⋅ cot θ + O Q 2 − O S 2 r cot θ + 2 r r r + 2 r 6 r ⟹ r = D G = D G = O G ⋅ cot 2 θ = cot 2 θ = 2 r 1 − r = 1 − r = 7 1 B e a u t i f u l ! Since r = tan θ
Therefore the ratio of the radius of the yellow circle to the radius of the red circle is 7 1 1 = 7 .
I always look forward to your solutions. This one is particularly good, I think.
Log in to reply
I also always look forward to your challenging problem. I have simplified the solution to make it more beautiful. Nice problem.
Let the radius of each red circle be 1 and let the radius of the yellow circle be r , so that the ratio of the radius of the yellow circle to the radius of a red circle is r , and label the diagram as follows:
△ H O I ≅ △ J O I by HL congruency, so ∠ H O I = ∠ J O I . Let θ = ∠ H O I = ∠ J O I .
Since the diagonals of a rhombus are perpendicular, ∠ D O C = 9 0 ° , and ∠ K O H = ∠ D O C − ∠ H O I − ∠ J O I = 9 0 ° − 2 θ , and from the angle sum of △ K H O makes ∠ K H O = 2 θ .
Since O H = O L + L H = r + 1 and O I = O F − I F = O F − H E = r − 1 , from △ H O I we have cos ∠ H O I = cos θ = r + 1 r − 1 .
Also, from △ K H O we have cos ∠ K H O = cos 2 θ = r + 1 1 .
Substituting cos θ = r + 1 r − 1 and cos 2 θ = r + 1 1 into the double angle identity cos 2 θ = 2 cos 2 θ − 1 gives r + 1 1 = 2 ( r + 1 r − 1 ) 2 − 1 , which rearranges to r ( r − 7 ) = 0 , and solves to r = 7 for r > 0 .