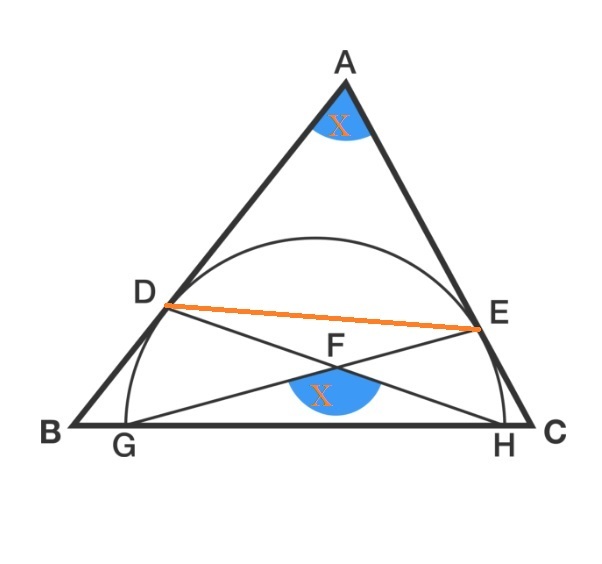
Inscribed Semicircle Riddle

Let O be the midpoint of GH and acting center of the semicircle. Then the radii OD & OE are perpendicular to BA and AC respectively.

Then let angle EGO = x. Then x = angle GEO due to isoscales property. Similarly, we'll obtain angle DHO = angle ODH = y.

Hence, angle FDA = 90-y and FEA = 90-x. We know that GFH = 180-x-y.

Thus, DAE= 360-(180-x-y)-(90-x)-(90-y) = 2x+2y.

Suppose s = x+y. Then GFH = 180-s and DAE=2s.

If they are equal, then 180-s=2s. Hence, s=60.

Finally, the desired blue angle = $2s =\boxed{120}$ .

By a circle theorem, if two tangents intersect in the exterior of a circle, then the measure of the angle formed is one half the difference of the measures of the intercepted arcs, so $\angle DAE = \frac{1}{2}(\overset{\frown}{DGE} - \overset{\frown}{DE})$ . Since $\overset{\frown}{DGE}$ is the whole circle except $\overset{\frown}{DE}$ , $\overset{\frown}{DGE} = 360° - \overset{\frown}{DE}$ , so $\angle DAE = \frac{1}{2}((360° - \overset{\frown}{DE}) - \overset{\frown}{DE})$ or $\angle DAE = 180° - \overset{\frown}{DE}$ . Rearranging gives $\overset{\frown}{DE} = 180° - \angle DAE$ .

By another circle theorem, if two chords intersect in the interior of a circle, then the measure of each angle is one half the sum of the measures of the arcs intercepted by the angle and its vertical angle, so $\angle GFH = \frac{1}{2}(\overset{\frown}{DE} + \overset{\frown}{GH})$ . Since $GH$ is a diameter, $\overset{\frown}{GH} = 180°$ , so $\angle GFH = \frac{1}{2}(\overset{\frown}{DE} + 180°)$ . Rearranging gives $\overset{\frown}{DE} = 2\angle GFH - 180°$ .

Since it is given that $\angle DAE = \angle GFH$ , then $\overset{\frown}{DE} = 180° - \angle DAE = 2 \angle DAE - 180°$ . Solving this gives $\angle DAE = \boxed{120°}$ .

In this solution i used some facts that i don't intend to prove, you can search for all of them on brilliant or any other website that contains geometry info.

Fact 1 : the angle from the arc $DE$ it's the suplementar of the $\angle BAC$

Fact 2 : $\angle DFE$ it's equal to $\angle GFH$ and also equal to $\frac{GH + DE}{2}$ ( $GH$ and $DE$ are arcs) so it's equal to $\frac{180 + DE}{2}$

So, this leaves us with:

$\angle BAC = \frac{180 + (180 - \angle BAC) }{2}$ , solving this leaves us with $BAC = 120$

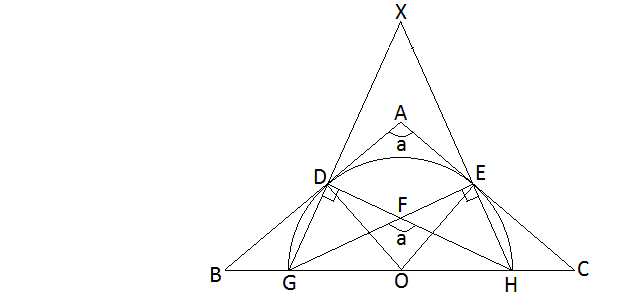
Since angles A and GFH are congruent, let's call them both 'x'.

Draw auxiliary line DE. Since AD and AE are tangents, they must be congruent, which makes triangle ADE isosceles.

Therefore, angle AED= (180-x)/2

Angle AED is also equal to 1/2 the measure of intercepted arc DE.

By substitution, the measure of arc DE is 180-x.

Angle GFH (x) is equal to 1/2 the sum of the arcs intercepted by it and it's vertical angle, DFE.

If we drew the rest of the circle, arc GH would be 180 degrees, since GH is a diameter.

This means x= 1/2(180+(180-x))

So 2x=360-x

3x=360

x=120

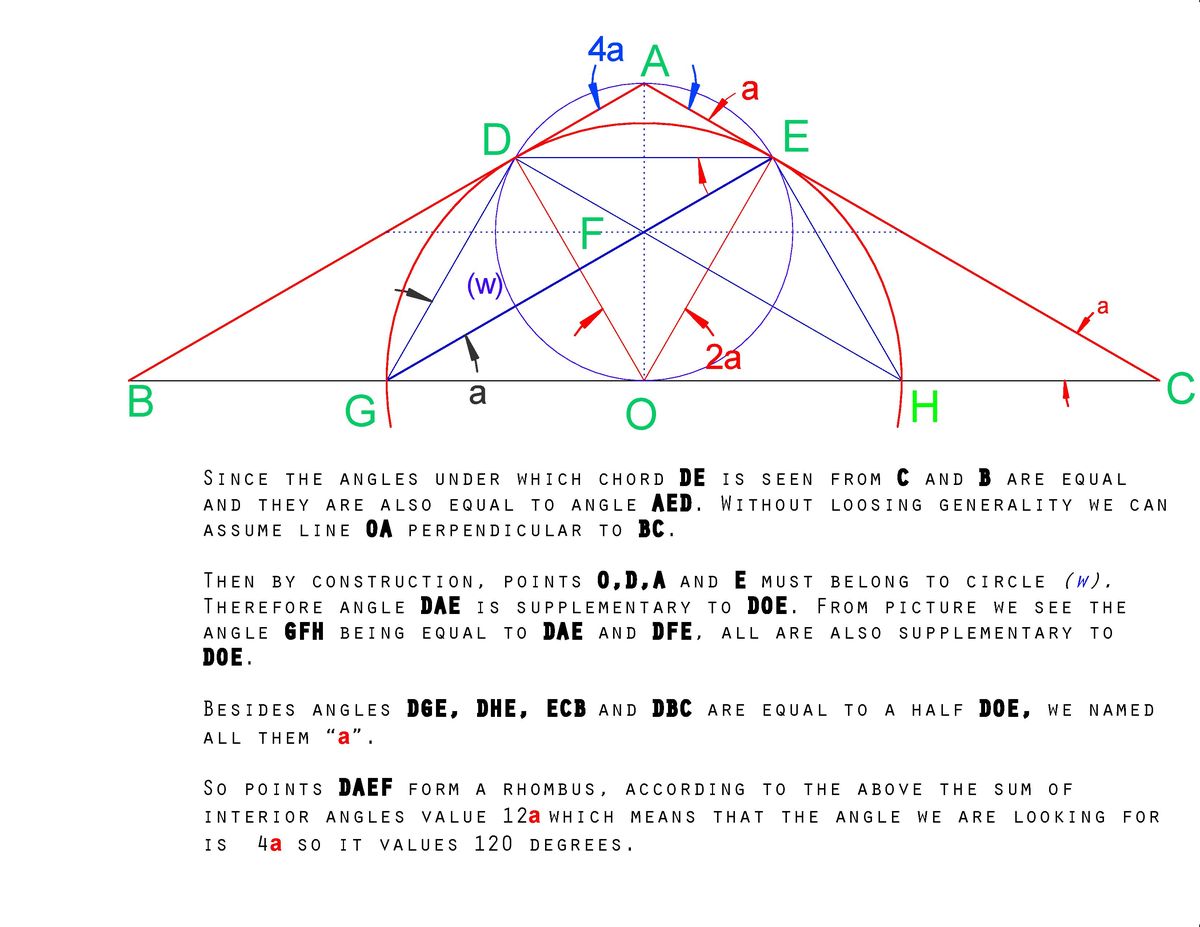
Let $O$ be the centre of semi-circle. Join $OD$ and $OE$ . Extend $GD$ and $HE$ to meet in $X$ . $OD \perp AD$ and $OE \perp AE$ , (since $AD$ and $AE$ are tangents to semi-circle) $\Rightarrow$ $ADOE$ is a cyclic quadrilateral. Let $\angle A = a$ .

Then $\angle DOE = 180^\omicron - \angle A = 180^\omicron - a$ ...(i)

$HD \perp XD$ and $GE \perp XE$ $\Rightarrow$ $XDFE$ is a cyclic quadrilateral. $\angle DFE = \angle GFH = \angle A = a$ $\Rightarrow$ $\angle DXE = 180^\omicron - a$ $\Rightarrow$ in $\triangle XGH \angle OGD + \angle OHE = a$ . ...(ii) $\angle ODG = \angle OGD$ and $\angle OEH = \angle OHE$

$\Rightarrow \angle DOG = 180^\omicron - 2\angle OGD$ and $\angle EOH = 180^\omicron - 2\angle OHE$ .

Adding both we get $\angle DOG + \angle EOH = 360^\omicron - 2(\angle OGD + \angle OHE ) = 360^\omicron - 2a$ [From (ii)]

Adding this equation and (i) we get, $\angle DOG + \angle DOE + \angle EOH = 540^\omicron - 3a = 180^\omicron$ [ since $GOH$ is a straight line ] Solving, we get $a = 120^\omicron$

$\large{\angle A =}$ $\angle GFH = \angle DFE = \angle GDH + \angle DGE = 90^{\circ}+ \angle AED = 90^{\circ} + (90^{\circ}- \frac{\angle A}{2}) \large{= 180^{\circ}- \dfrac{\angle A}{2}}$

$\large{\Rightarrow \angle A = 120^{\circ}}$