Inscribed square

Geometry Level 3

We inscribed the red square into a bigger square, as it is shown in the figure below. The lengths of the bigger square are 10 10 .

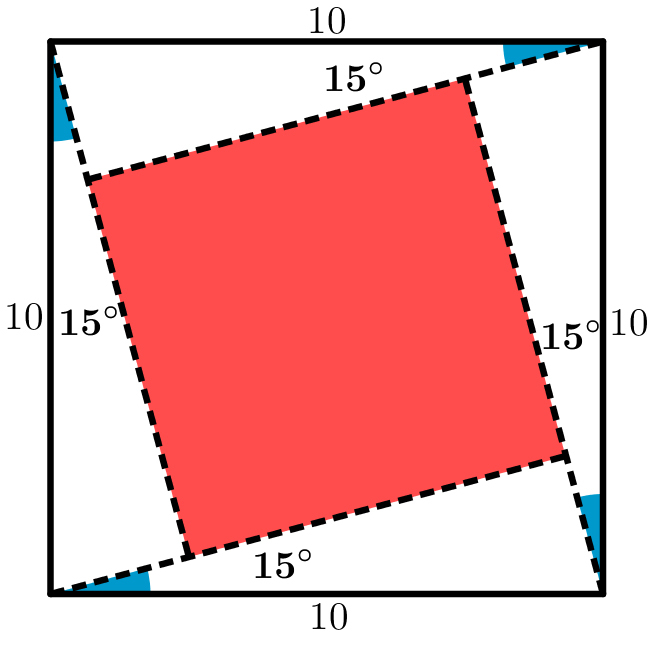
What is the area of the smaller, red square?

60 None of the others 50 70 40

View wiki
Áron Bán-Szabó by Áron Bán-Szabó , 17, Hungary

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

1 solution

The area of each of the 4 peripheral triangles is 1 2 ( 10 sin ⁡ ( 1 5 ∘ ) ) ( 10 cos ⁡ ( 1 5 ∘ ) ) = 50 sin ⁡ ( 1 5 ∘ ) cos ⁡ ( 1 5 ∘ ) = 25 sin ⁡ ( 3 0 ∘ ) = 12.5 \dfrac{1}{2}(10\sin(15^{\circ}))(10\cos(15^{\circ})) = 50\sin(15^{\circ})\cos(15^{\circ}) = 25\sin(30^{\circ}) = 12.5 ,

where the identity sin ⁡ ( 2 x ) = 2 sin ⁡ ( x ) cos ⁡ ( x ) \sin(2x) = 2\sin(x)\cos(x) was used. Thus the sum of the areas of the 4 peripheral triangles is 4 × 12.5 = 50 4 \times 12.5 = 50 , and so the area of the red square is 1 0 2 − 50 = 50 10^{2} - 50 = \boxed{50} .

3 Helpful 0 Interesting 0 Brilliant 0 Confused

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...