Inscribed To Infinity
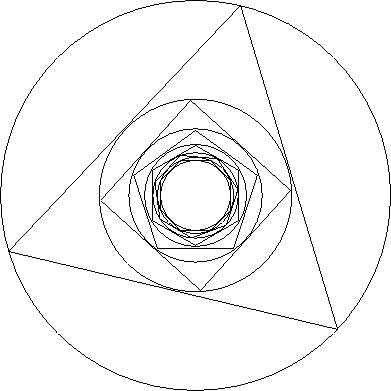 Take a circle of radius 1. Inscribe a regular triangle in this circle. Inscribe a circle in this triangle. Inscribe a square in it. Inscribe a circle, regular pentagon, circle, regular hexagon and so forth.
Take a circle of radius 1. Inscribe a regular triangle in this circle. Inscribe a circle in this triangle. Inscribe a square in it. Inscribe a circle, regular pentagon, circle, regular hexagon and so forth.
What is the radius of the circle formed when the process is carried forever (the radius of the limiting circle)?
Give the answer correct to 3 decimal places.
You might also like this .
The answer is 0.114.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
Moderator note:
Well done!
I calculated by hand until the radius of the 90th circle: 0.1211718
In the end I used wolfram Alpha...
It looks really cool by the way: Here
Log in to reply
How did u calculate the 90th by hand. That's insane.
Yea I tried doing the last step with a calculator to but it wouldn't converge fast enough
Please Post Solution Here ... @Digvijay Singh
Solving this for hours then I found out that this was only a constant XD
Kepler-Bouwkamp constant.
Got on Wikipedia
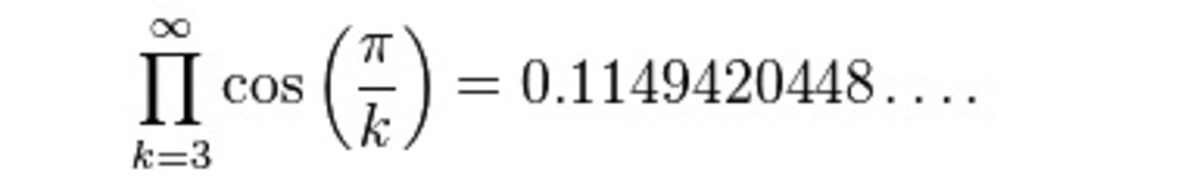
Can anyone see a nice way to solve this analytically?
I reluctantly gave up and used Python to approximate the product series
n = 3 ∏ n = 1 0 0 0 0 0 0 0 sin ( 2 n ( n − 2 ) π ) = 0 . 1 1 4 9 4 2 1 0 1 5 7 4 7 3 3 5 6
Here is the code :
import numpy as np
def product_series(N):
product = 1.0
for i in range(3,n+1):
product*= np.sin((n-2)*np.pi/(2*n))
return product
product_series(10000000)
I did the same with excel. got answer 0.115.
It's possible to get this in terms of the Riemann zeta function, but I have no idea how.
The equation relating the inradius and the circumradius of a regular polygon, r = R cos ( n π ) gives the ratio of the radii of the final to initial circles as K ′ = r initial circle r final circle = cos ( 3 π ) cos ( 4 π ) cos ( 5 π ) ⋯ Numerically, K ′ = K 1 = 8 . 7 0 0 0 3 6 6 2 5 2 1 = 0 . 1 1 4 9 4 2 0 4 4 8