Inscribed Truncated Cone.
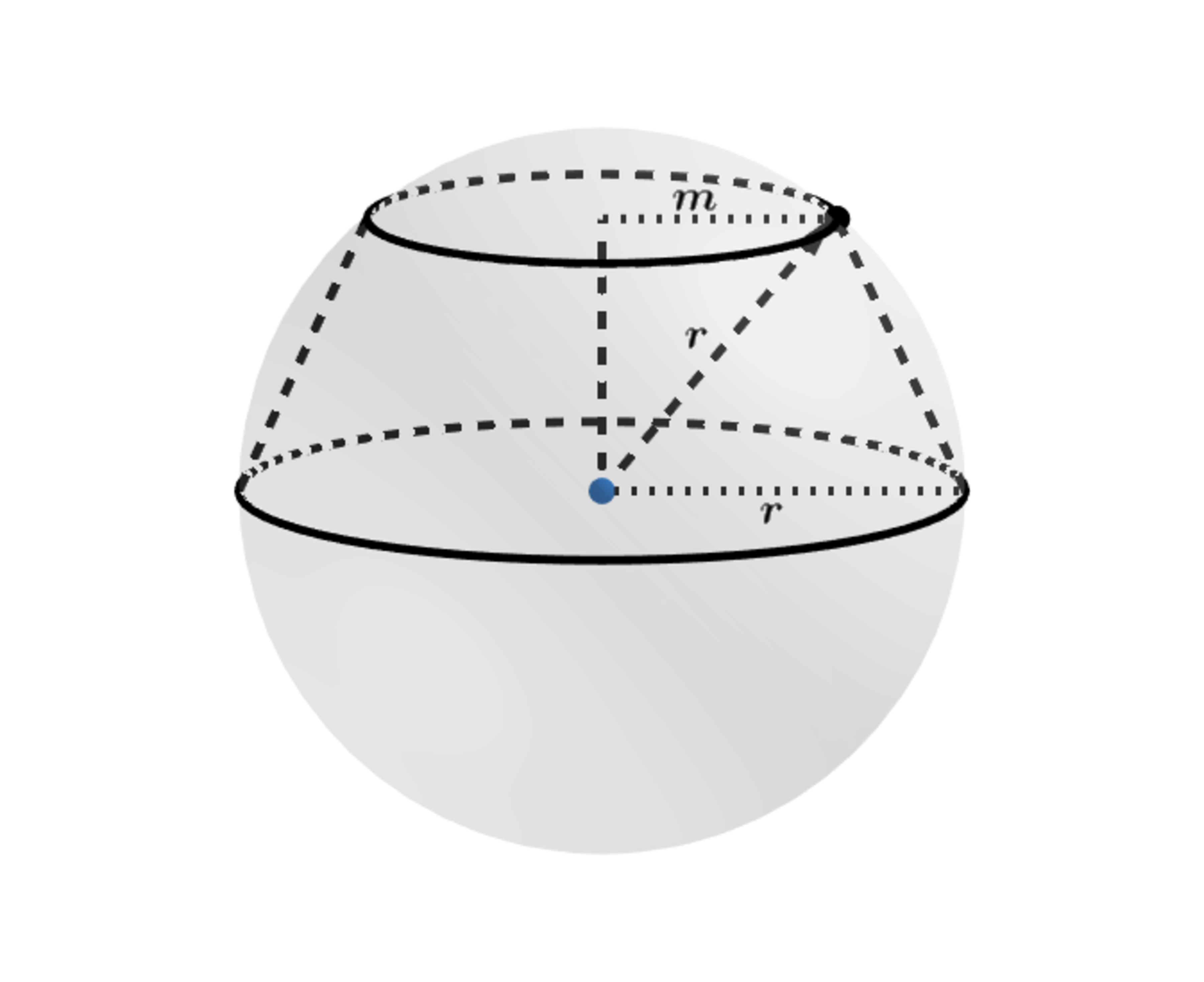
In the diagram above, a truncated cone is inscribed in a sphere of radius such that the larger base of the truncated cone is a great circle of the sphere.
Let be the radius of the smaller base.
Find the ratio that maximizes the volume of the inscribed truncated cone as described above.
The answer is 0.646488.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
m = r cos ( θ ) and h = r sin ( θ )
⟹ the volume of the truncated cone V = 3 π ( r 2 + r 2 cos ( θ ) + r 2 cos 2 ( θ ) ) r sin ( θ ) =
3 π r 3 ( 2 sin ( θ ) + 2 1 sin ( 2 θ ) − sin 3 ( θ ) )
⟹ d θ d V = 3 π r 3 ( 2 cos ( θ ) + cos ( 2 θ ) − 3 sin 2 ( θ ) cos ( θ ) ) =
3 π r 3 ( 2 cos ( θ ) + 2 cos 2 ( θ ) − 1 − 3 ( 1 − cos 2 ( θ ) ) cos ( θ ) )
⟹ 3 cos 3 ( θ ) + 2 cos 2 ( θ ) − cos ( θ ) − 1 = 0
Let u = cos ( θ ) ⟹ 3 u 3 + 2 u 2 − u − 1 = 0
To solve the cubic:
To eliminate the square term let u = w − 9 2
⟹ 7 2 9 w 3 − 3 5 1 w − 1 7 3 = 0 ⟹ w 3 − 2 7 1 3 w − 7 2 9 1 7 3 = 0
Let w = z + 8 1 z 1 3 ⟹ 5 3 1 4 4 1 z 6 − 1 2 6 1 1 7 2 z 3 + 2 1 9 7 = 0 ⟹
z 3 = 1 4 5 8 1 7 3 + 2 7 2 9 = R = R ( cos ( 2 π n ) + i sin ( 2 π n ) ) ⟹
z = R 3 1 ( cos ( 3 2 π n ) + i sin ( 3 2 π n ) ⟹
z = R 3 1 , R 3 1 ( − 2 1 ± i 2 3 )
In this case we have exactly one real root for 3 u 3 + 2 u 2 − u − 1 = 0
Using z = R 3 1 ⟹ w = R 3 1 + 8 1 R 3 1 1 3 ⟹
u = R 3 1 R 3 2 − 9 2 R 3 1 + 8 1 1 3 = cos ( θ ) ≈ 0 . 6 4 6 4 8 8
m = r cos ( θ ) ⟹ r m = 0 . 6 4 6 4 8 8 .
Checking for relative max at θ = θ 0 .
Incidentally θ 0 ≈ 0 . 8 6 7 8 2 4 radians.
cos ( θ ) = 0 . 6 4 6 4 8 8 ⟹ sin ( θ ) = 1 − cos 2 ( θ ) = 0 . 7 6 2 9 2 4
and
d θ 2 d 2 V ∣ θ = θ 0 = 3 π r 3 sin ( θ ) ( − 9 cos 2 ( θ ) − 4 cos ( θ ) + 1 ) ∣ θ = θ 0 = − 4 . 7 9 7 1 5 < 0
⟹ relative max at θ = θ 0 .
Quick Note: In solving the cubic above I used the following method:
Given: a x 3 + b x 2 + c x + d = 0 we let x = u − 3 a b to eliminate the square term.
This results in the cubic: u 3 + P u + Q .
Letting u = z − 3 z P we obtain a quadratic in z 3 as was the case above.