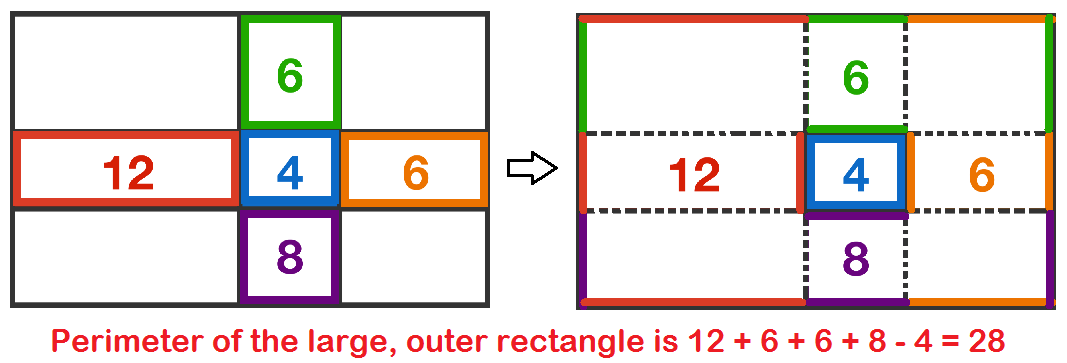
Inside perimeters
A rectangle is divided into nine sub-rectangles, as shown in the figure. Inside some rectangles are their respective perimeters .
What is the perimeter of the large, outer rectangle?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
13 solutions
Wow, I use another method, this is clever! Or 12+6+6+8+4-4-4 ? demonstrated by the graph?
Log in to reply
No need to remove 4 two times: 4 is already a sum of the four sides. Really clever, I didn't think of doing it this way neither!
I didn't even think of doing it that way! Nicely illustrated. Thank you.
That is nice! I went like this - if the sides are all integers, the central quadrilateral has to be a square with side length 1 (since 2 of its sides will have total length 2, and this can only be true if both have a length of 1). Then it is easy to calculate the side lengths for all the other sub-rectangles as well. You end up with length of the big rectangle = 5+1+2, and width = 2+1+3. Thus the perimeter is 14 x 2 = 28. Not a particularly elegant solution, but a simple one.
Log in to reply
This is how I did it as well. the centre rectangle has to be square, with each side having length equals 1. You can then infer what the dimensions of the other coloured rectangles have to be since the edge they share with the centre rectangle has to be equal to 1.
need to find only the semi périmètre of All four black rectangle and add the center blues rectangle perimeter: left high black semi perimeter is ((12+6)-4)/2 = 7 + left low black semi perimeter is ((12+8)-4)/2. = 8 + right higth black semi perimeter is ((6+6)-4)/2 = 4 + right high black semi perimeter is ((6+8)-4)/2 = 5 + blue périmètre = 4 =28 ;)
I tried to eyeball the measurement. I think drawing a diagram works best. Next time I should try to actually draw it again. I would rate this problem a 2 because I already know how perimeter works. I wanted to try eyeballing it. But I think it's better to redraw it.
That took me several minutes to understand, but once I did, I realized how beautifully elegant your answer was. Bravo!
it's so easy to find the solution, when you think that the "4" rectangle is a square, but to accept the solution first you should explain why the "4" rectangle is a square.
Log in to reply
the "4" rectangle is not necessarily a square.
Log in to reply
No , the "4" rectangle will be a square , perimeter of a rectangle = 2(l + b)
2(l + b) = 4
l + b = 2
So, both l and b will be 1 because their sum add up to 2 . So now opposites sides in a rectangle are equal so all the four sides are equal to 1 and therefore it is a square .
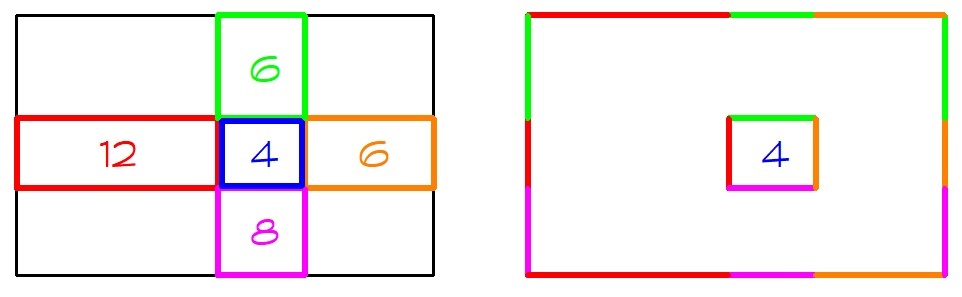 The perimeter of the large, outer triangle (see the figure on the right) is composed of 3 three red lines, three green lines, three orange lines and three violet lines. The total perimeter of the three smaller rectangles (see the figure on the left;exclude the blue rectangle) is 12+6+6+8=32 and it is composed of four red lines, four green lines, four orange lines and four violet lines. So to get the perimeter of the biggest rectangle we need to subtract one red line, one green line, one orange line and one violet line. And that is exactly the perimeter of the blue rectangle (see left figure). Therefore, the desired answer is 32-4=28.
The perimeter of the large, outer triangle (see the figure on the right) is composed of 3 three red lines, three green lines, three orange lines and three violet lines. The total perimeter of the three smaller rectangles (see the figure on the left;exclude the blue rectangle) is 12+6+6+8=32 and it is composed of four red lines, four green lines, four orange lines and four violet lines. So to get the perimeter of the biggest rectangle we need to subtract one red line, one green line, one orange line and one violet line. And that is exactly the perimeter of the blue rectangle (see left figure). Therefore, the desired answer is 32-4=28.
Nicely explained! Thank you.
Notice that we can identify each green/red/orange/purple side with a black side, so the perimeters of the green/red/orange/purple rectangles cover the perimeter of the black rectangle. However, there are 4 colored sides left over - but they each can be identified with a side of the blue rectangle. So the black rectangle's perimeter is: ( 6 + 1 2 + 6 + 8 ) − 4 = 2 8
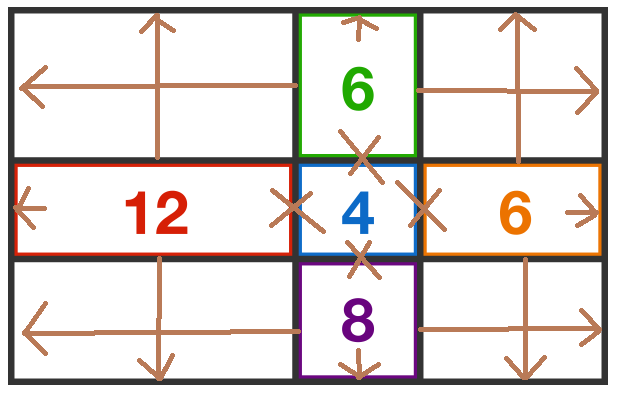
Simpler to assume that the central box is 1 x 1 and calculate all others. e.g. the 12 box must be 1 x 5, the 8 box is 1 x 3, etc.
Log in to reply
Yes, but that is not necessarily true. It is possible that the dimensions of the inner blue shape are 1.5 and 0.5, not 1 and 1.
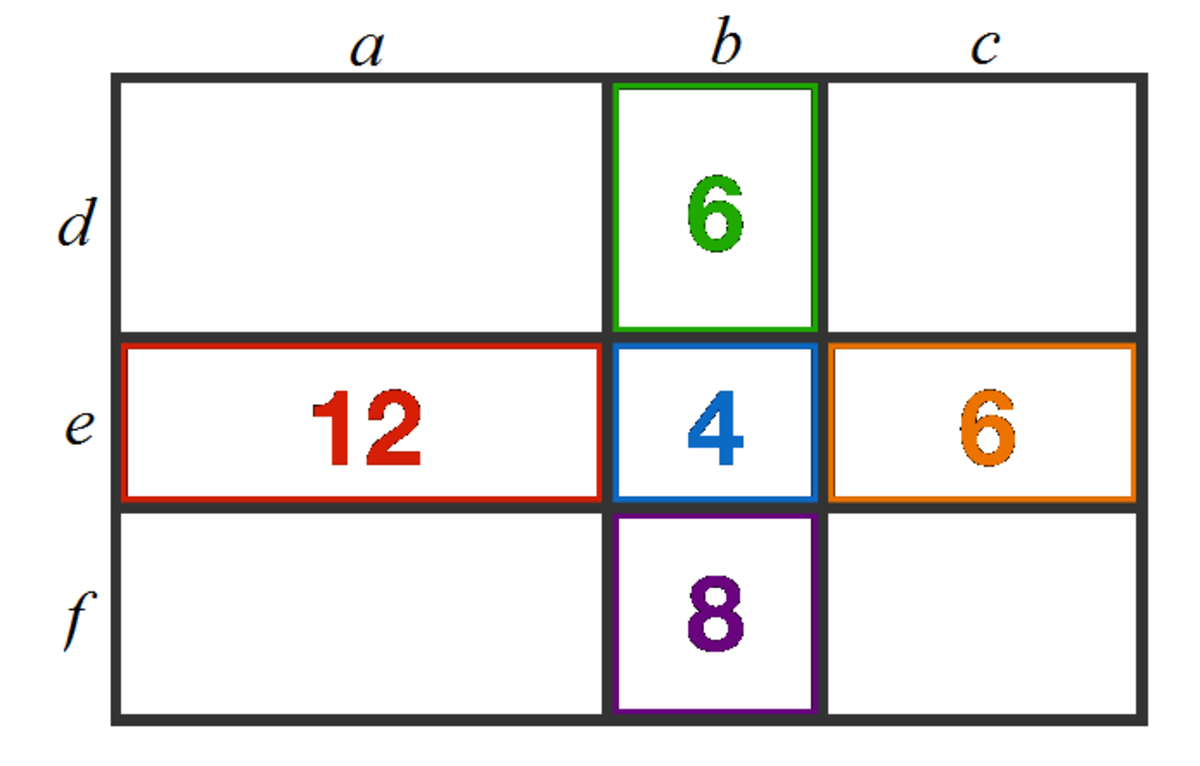
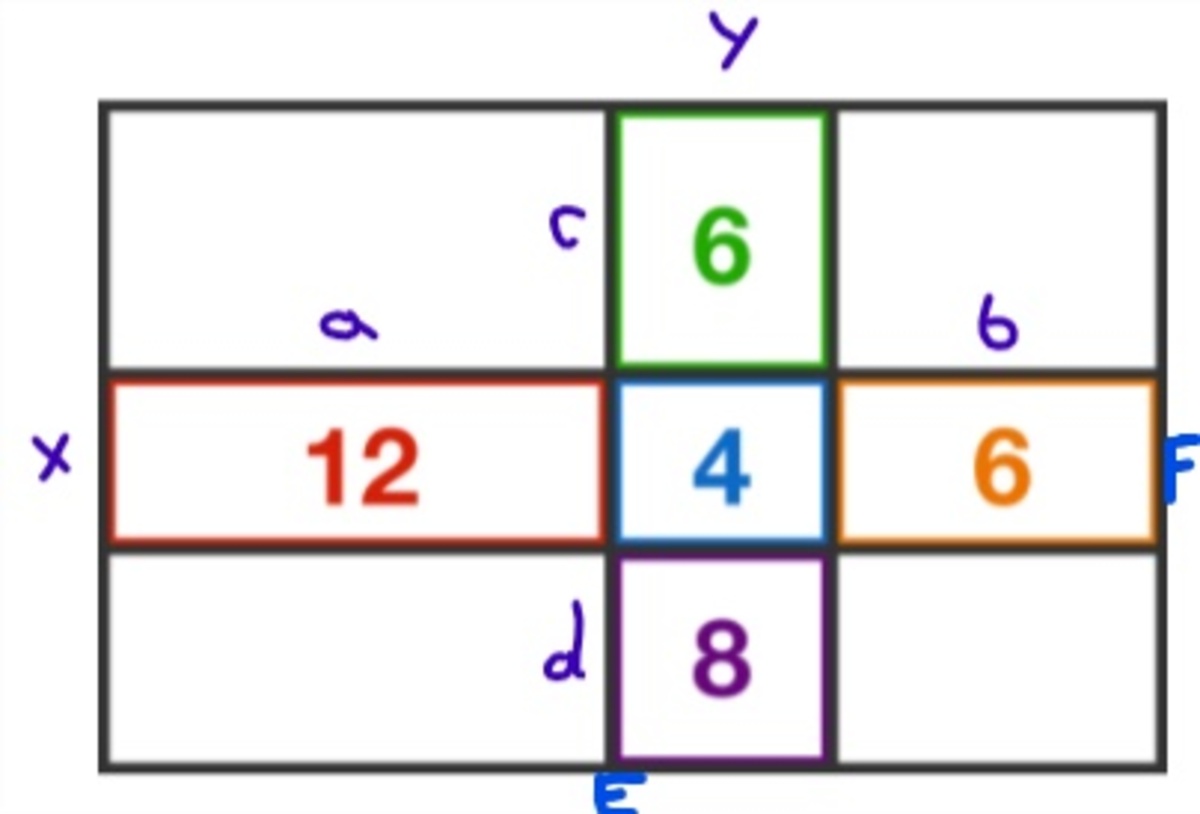
Let the side lengths be assigned as a , b , c , d , e and f as shown in the figure. Then the parameter of the the larger, outer rectangle is given by p = 2 ( a + b + c + d + e + f ) and we have:
⎩ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎨ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎧ 2 a + 2 e = 1 2 2 b + 2 d = 6 2 b + 2 e = 4 2 b + 2 f = 8 2 c + 2 e = 6 . . . ( 1 ) . . . ( 2 ) . . . ( 3 ) . . . ( 4 ) . . . ( 5 )
Adding ( 1 ) + ( 2 ) + ( 3 ) + ( 4 ) + ( 5 ) , we have:
2 a + 6 b + 2 c + 2 d + 6 e + 2 f 2 a + 2 b + 2 c + 2 d + 2 e + 2 f + 4 b + 4 e 2 ( a + b + c + d + e + f ) p = 1 2 + 6 + 4 + 8 + 6 = 3 6 − 3 6 = 3 6 − 2 ( 2 b + 2 e ) = 3 6 − 2 ( 4 ) = 2 8 ( 3 ) : 2 b + 2 e = 4
Nice job. I like your relatively rigorous method/explanation best (you accidently forgot an "= 0" in the 3rd to last line). I was headed down the same path when I realized the perimeter of the cross formed by the 5 given tiles is equivalent to the perimeter of the outer rectangle, similar to other methods posted. It is apparent that the perimeter of the cross formed by the 5 given tiles is the perimeter of each outer tile (12,6,6,8) minus the center tile (4).
Log in to reply
Thanks, but @Venkatachalam J 's solution is better.
Log in to reply
I wouldn't say better or worse, just different. Most people saw the "trick" geometrically, you algebraically.
I try something like that at first too, but I was too lazy to go that path! :D Nicely done sir!
Dumbest, yet the fastest method: This response is based on an assumption, which is that the rectangle with a perimeter of 4 has side lengths of 1, therefore making it a square. Hence, you can easily find the side length and width of the larger rectangle being 8 and 6 respectively. Add them up and multiply by 2, and you'll get 28.
Maybe the dumbest, but that’s what I did.
Using mental arithmetic too!
Like Ananda says, it is the dumbest and technically wrong unless you check solution, but of course it is what I did as well. Upvote for common answer
I find issue with the fact that the box with a perimeter or 8 is smaller than the ones with 6...
Me too, I know if was faulty solution but still celebrated the “win”. I am interested to know when this faux solution would fail to get the right answer. Is it to do with the internal perimeters, vertical and horizontal conveniently being nice easy multiples of each other?
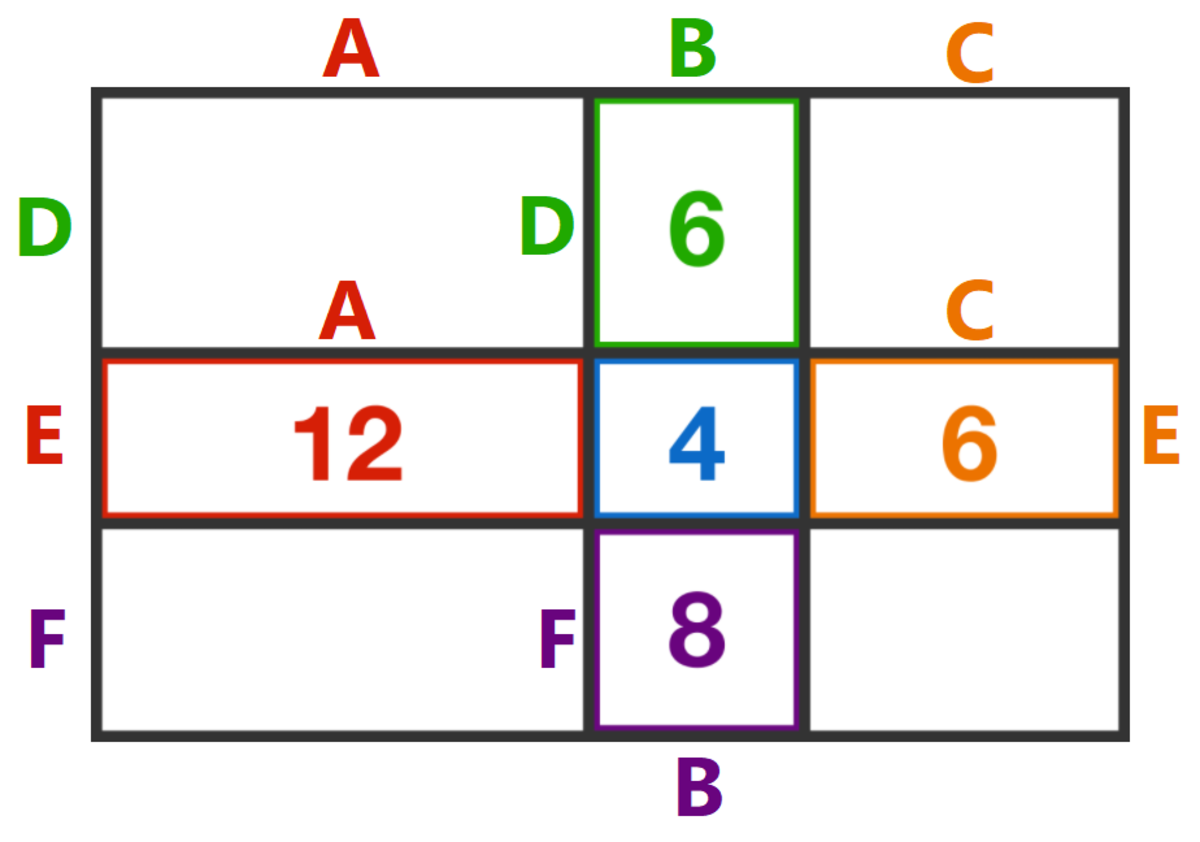
Two side lengths of a rectangle add to half the perimeter of that rectangle, so:
B + D = 6 ÷ 2 = 3
A + E = 1 2 ÷ 2 = 6
C + E = 6 ÷ 2 = 3
B + F = 8 ÷ 2 = 4
Add these up to get A + 2 B + C + D + 2 E + F = 1 6 .
Also, note that the two blue rectangle side lengths are B and E .
B + E = 4 ÷ 2 = 2
Subtract this new equation from the last to get:
A + B + C + D + E + F = 1 4
The total perimeter is 2 × 1 4 = 2 8 .
how is it?
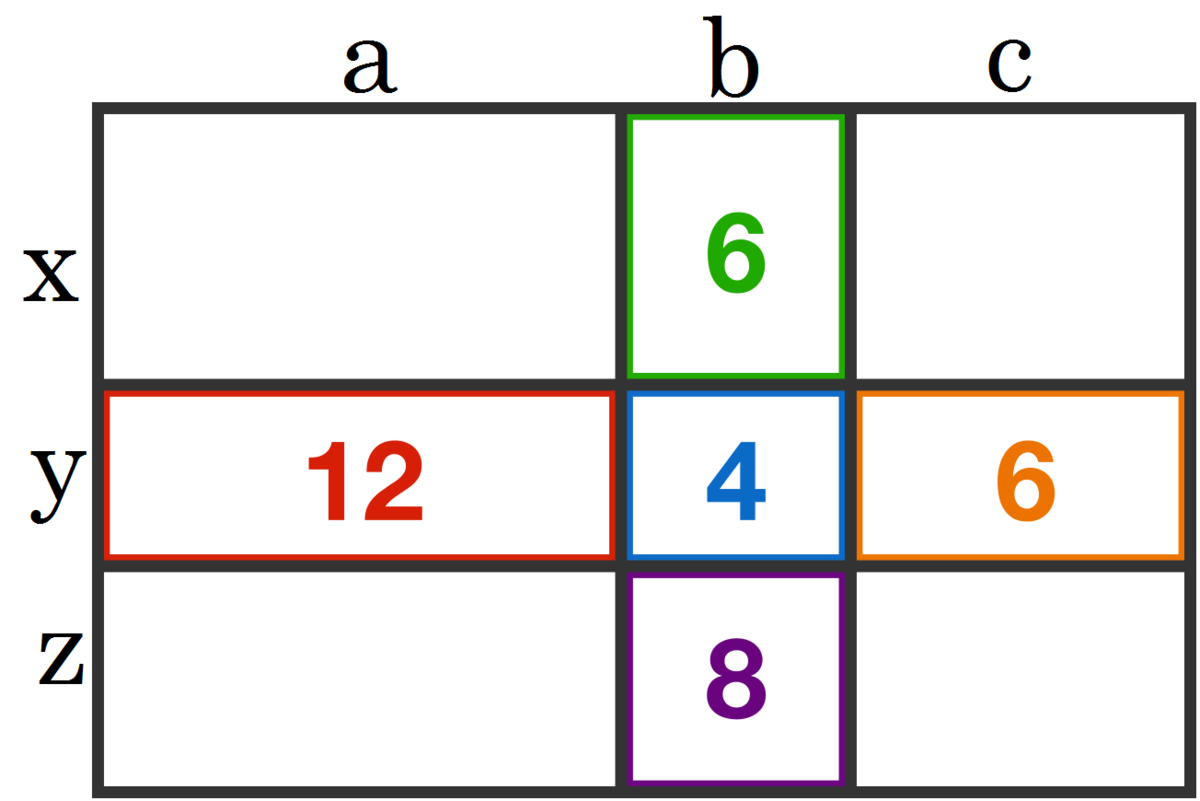
So we are looking for 2 ( x + y + z ) + 2 ( a + b + c ) which is also equivalent to 2 a + 2 b + 2 c + 2 x + 2 y + 2 z
2 y + 2 a = 1 2
2 x + 2 b = 6
2 y + 2 b = 4 ⇒ 4 y + 4 b = 8
2 z + 2 b = 8
2 c + 2 y = 6
Adding all the equations, we get:
2 a + 6 b + 2 c + 2 x + 6 y + 2 z = 3 6
And we are looking for 2 a + 2 b + 2 c + 2 x + 2 y + 2 z , so we subtract 4 y + 4 b from 2 a + 6 b + 2 c + 2 x + 6 y + 2 z :
2 a + 2 b + 2 c + 2 x + 2 y + 2 z = ( 2 a + 6 b + 2 c + 2 x + 6 y + 2 z ) − ( 4 y + 4 b )
2 a + 2 b + 2 c + 2 x + 2 y + 2 z = 3 6 − 8
2 a + 2 b + 2 c + 2 x + 2 y + 2 z = 2 8
I start with the inner rectangle. I can see it has, as one solution, equal sides of 1 unit each. I can then determine the remaining lengths:
(6-1-1)/2=2
(8-1-1)/2=3
(12-1-1)/2=5
I can now calculate the larger perimeter:
2((5+1+2) + (2+1+3))=28
This result can be checked by assigning different values to the original rectangle.
I'm glad I'm not the only one who figured it out this way
Lol, I didn't think of rearranging the walls and I just proved it mathematicly XD
 x+y=
3
1
(x+a)=
3
2
(x+b)
Therefore: E = 3(x+y)+x+y+
2
3
(x+y)= ... =
1
6
1
5
x+
2
1
1
b
AND
x+y=
3
2
(y+c)=
2
1
(y+d)
Therefore: F =
2
3
(x+y)+x+y+2(x+y)= ... =
2
9
+
2
3
b
Perimeter = 2E+2F=5x+11y+9x+3y=14x+14y
If 4=2x+2y then 2=x+y and y=2-x
Perimeter=14x+14(2-x)=14x-14x+28=
28
x+y=
3
1
(x+a)=
3
2
(x+b)
Therefore: E = 3(x+y)+x+y+
2
3
(x+y)= ... =
1
6
1
5
x+
2
1
1
b
AND
x+y=
3
2
(y+c)=
2
1
(y+d)
Therefore: F =
2
3
(x+y)+x+y+2(x+y)= ... =
2
9
+
2
3
b
Perimeter = 2E+2F=5x+11y+9x+3y=14x+14y
If 4=2x+2y then 2=x+y and y=2-x
Perimeter=14x+14(2-x)=14x-14x+28=
28
Perimeter of Rectangle = 2(l+b)
It could be several different answers. The perimeters are given but it doesn't say the sides must be whole. What if the middle rectangle is .5x1.5? The answer could be 30. If the drawing is in perfect scale, there is no way all of the sides are whole numbers.
True. But even with decimals. The length would be 9.5 and the width 4.5.
P=2(9.5+4.5) P still equals 28
The heights for all the middle "rectangles" are 0. Those are lines. The scaling for this diagram is atrocious.