Inspiration
In a square A B C D , two lines are drawn such that one of them connects point A to opposite corner C while the other line joins point B to the midpoint E of side C D . Now these two lines meet at a point F inside the square A B C D . If quadrilateral A D E F has an area of 20, determine the area of △ C E F ?
The answer is 4.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
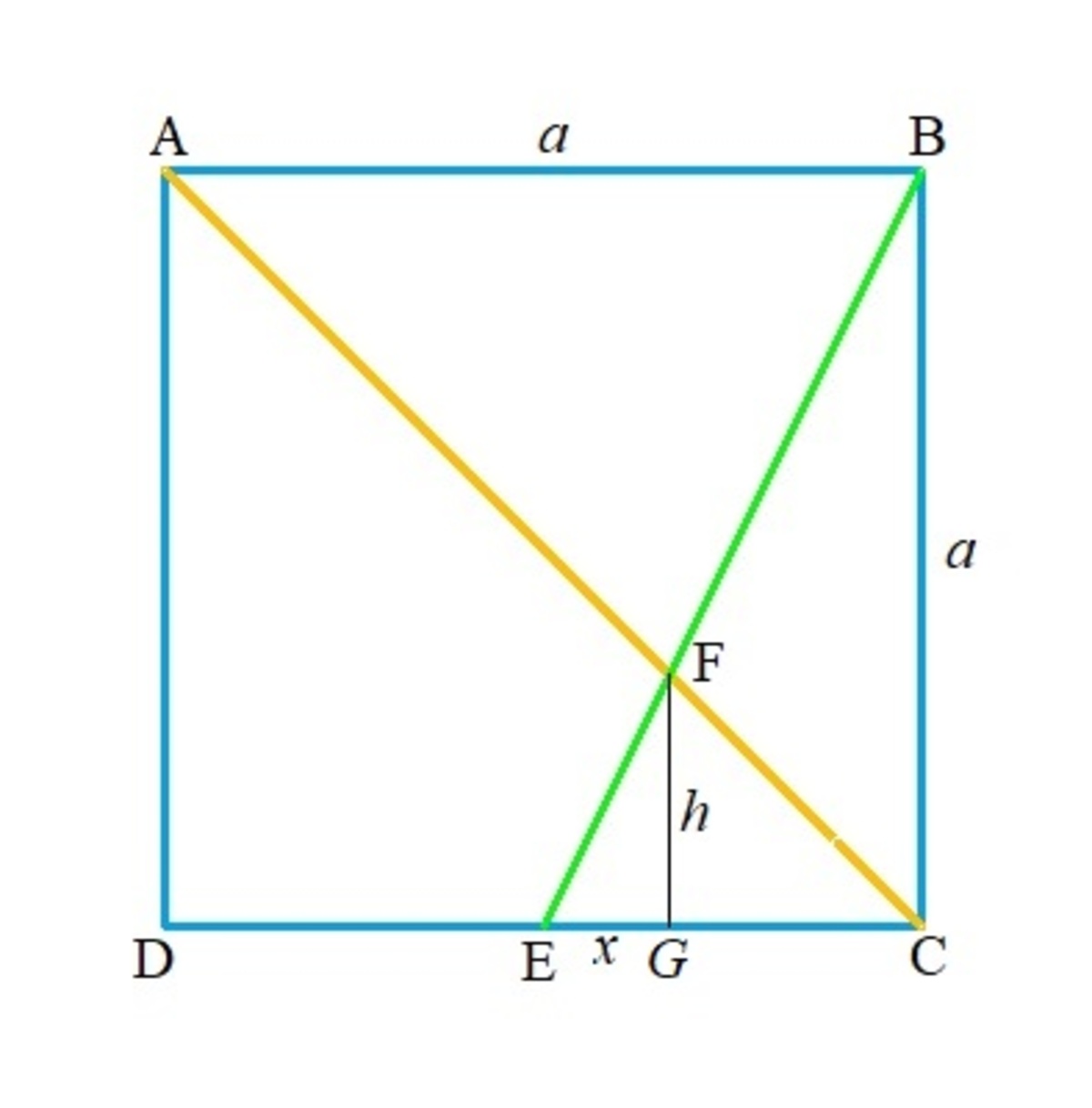
Let the side length of square A B C D be a , the altitude of △ C E F , F G = h and E G = x . Then we note that h = 2 x = 2 a − x ⟹ x = 6 a ⟹ h = 3 a . Then the area of △ C E F = 2 1 × h × 2 a = 1 2 a 2 . We note that:
[ A C D ] 2 a 2 1 2 5 a 2 ⟹ 1 2 a 2 = [ A D E F ] + [ C E F ] = 2 0 + 1 2 a 2 = 2 0 = 4
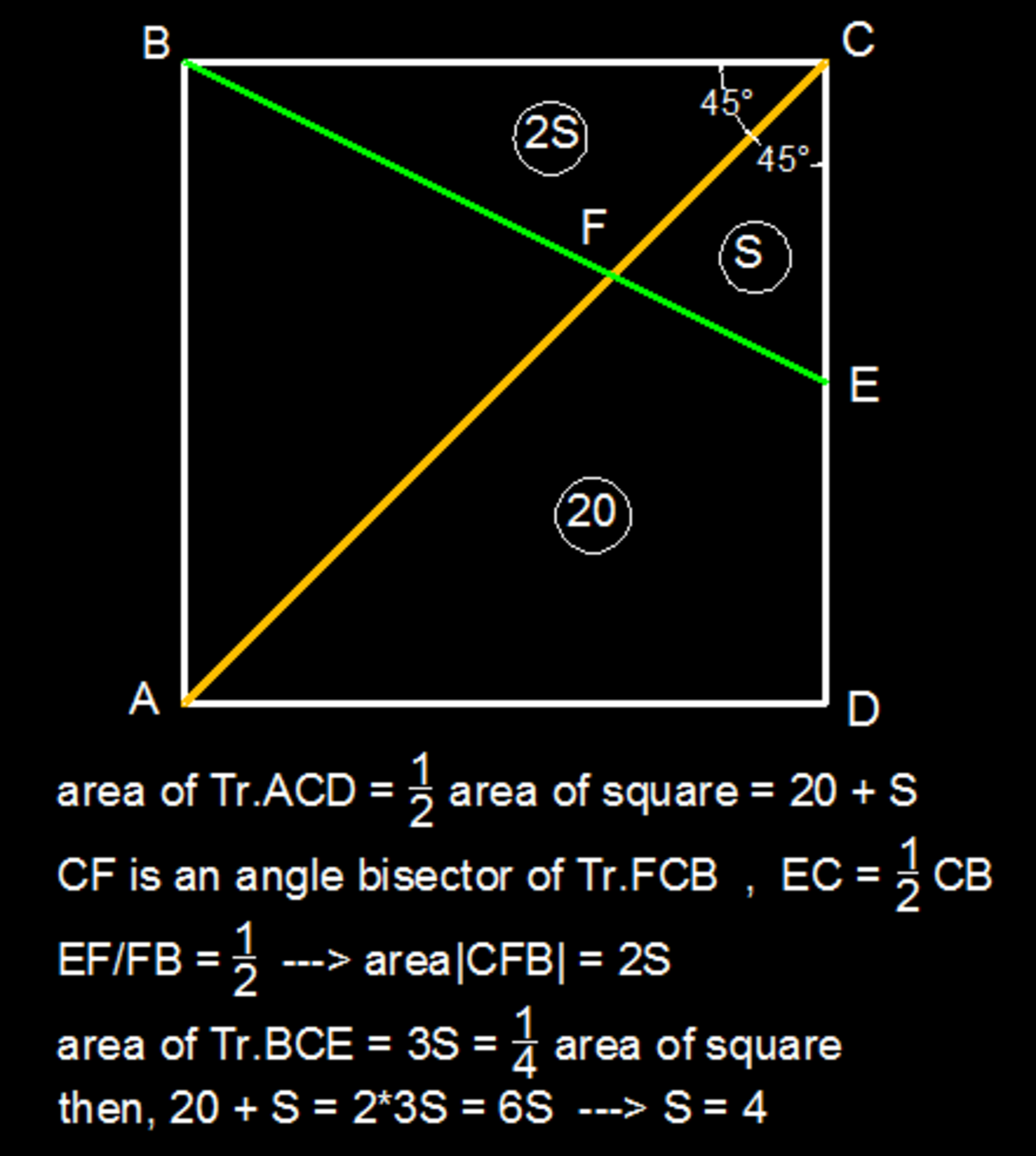
We let the area of △ C E F = x . Now what should the area of △ B C F be in terms of x ? Drop a perpendicular from F to B C and another from F to C E . Suppose these perpendicular touch B C at G and C E at H . Considering that ∠ C G F = ∠ C H F = 9 0 degrees, ∠ G C F = ∠ H C F = 4 5 degrees and that C F is common to both △ C F G and △ C F H , it follows that these two triangles are congruent. Therefore F G = F H .
Then considering that A B C D is a square, B C = C D and considering that E is the midpoint of C D , C D = 2 C E . Therefore B C = 2 C E which means △ B C F has twice the base of △ C E F . Considering that both triangles have the same perpendicular height ( F G = F H ) , △ B C F has twice the area of △ C E F or 2 x .
Then the area of △ B C E is the sum of that of △ B C F and that of △ C E F which gives us 2 x + x = ( 2 + 1 ) x = 3 x . Then △ A C D would be twice the area of △ B C E as both share the same height of A D = B C but C D = 2 C E . Therefore the area of △ A C D = 2 ( 3 x ) = ( 2 × 3 ) x = 6 x .
Finally, △ A C D can be partitioned into △ C E F and quadrilateral A D E F . Therefore, the area of quadrilateral A D E F can be expressed as the area of △ A C D minus the area of △ C E F which is 6 x − x = ( 6 − 1 ) x = 5 x .
Therefore,
5 x = 2 0
x = 4