Inspirception
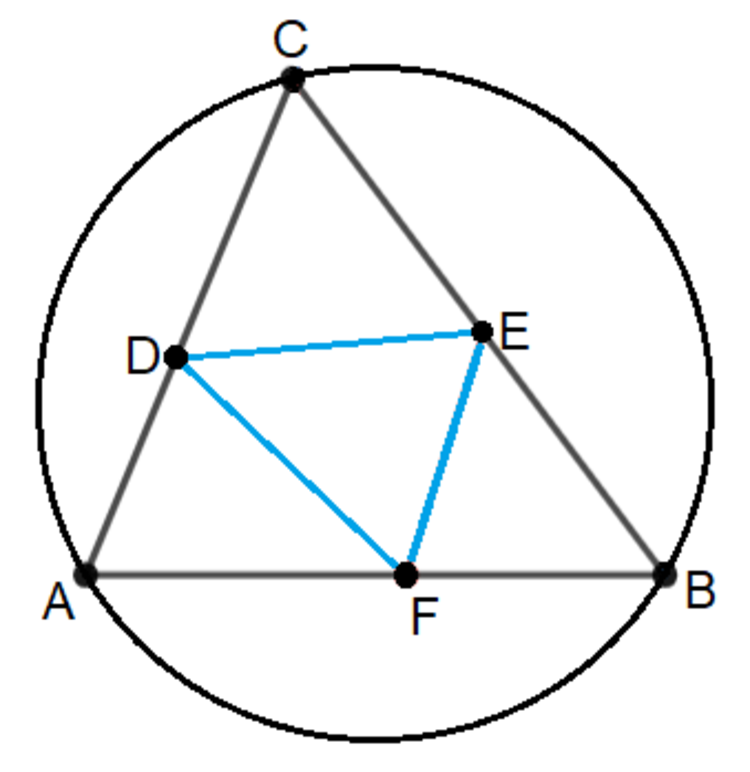 △
A
B
C
is an acute triangle with a circumradius of
2
5
and
△
D
E
F
is constructed by placing one vertex on each side of
△
A
B
C
. If the smallest possible perimeter of
△
D
E
F
is
5
6
, find the area of
△
A
B
C
.
△
A
B
C
is an acute triangle with a circumradius of
2
5
and
△
D
E
F
is constructed by placing one vertex on each side of
△
A
B
C
. If the smallest possible perimeter of
△
D
E
F
is
5
6
, find the area of
△
A
B
C
.
Inspiration of the Inspiration
The answer is 700.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
Great solution! I believe you meant to say that points D 1 , E , F , and D 2 are collinear, though, not D 1 , E , F , and E 2 .
Reflect △ A B C in C B and then reflect △ A ′ B C in C A ′ .
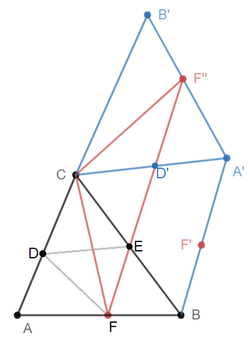
Then the perimeter of △ D E F is equivalent to F E + E D ′ + D ′ F ′ ′ , which is at a minimum when E and D ′ are on F F ′ ′ .
Since reflections preserve lengths and angles, △ A B C ≅ △ A ′ B C ≅ △ A ′ B ′ C , so C F = C F ′ ′ and ∠ F C F ′ ′ = 2 ∠ A C B .
By the law of cosines on △ F C F ′ ′ , F F ′ ′ = C F 2 + C F 2 − 2 ⋅ C F ⋅ C F cos 2 ∠ A C B = 2 ⋅ C F ⋅ sin A C B .
Since 2 ⋅ sin A C B is a positive constant, F F ′ ′ reaches a minimum when C F is a minimum, which is when C F is the altitude of △ A B C . Therefore, the minimum perimeter is P min = 2 h c sin C , where h c is the altitude of △ A B C from C .
Using triangle area equations T = 2 1 h c c and T = 2 1 a b sin C , we get P min = a b c 8 T 2 , and using the circumradius equation R = 4 T a b c , we get T = 2 1 R P min .
In this question, R = 2 5 and P min = 5 6 , so T = 2 1 ⋅ 2 5 ⋅ 5 6 = 7 0 0 .
If DEF has the smallest possible perimeter then we know that it's the orthic triangle in which case, R r = P e r i m e t e r o f △ A B C P e r i m e t e r o f △ D E F or r x Perimeter of △ABC = 56 x 25 or Semi-perimeter of △ABC x r =28 x 25 = 700 s.u.
I couldn't solve this without cheating. Like this: For a given reference triangle ( △ A B C ), its orthic triangle ( △ D E F ) produces the minimum perimeter. I placed three points on a Geogebra circumcircle until its orthic triangle was close to 56. It was surprisingly easy.
Anyway, I just wanted to say this is a great problem! Thank you, David.
Reflect D and E in A B (note I have labelled the vertices of the transcribed circle more conventionally) to obtain points D 2 and E 1 . Reflect E and F in B C to obtain E 2 and F 1 . Finally reflect F and D in A C to obtain F 2 and D 1 . Note that distances D 1 E + E F + F D 2 = E 1 F + F D + D E 2 = F 1 D + D E + E F 2 = D E + E F + F D = P are all equal, where P is the perimeter of the triangle D E F , and so we will have the shortest perimeter P for the inscribed triangle D E F if we can choose points D , E , F such that the points D 1 , E , F , D 2 are collinear, as well as the points E 1 , F , D , E 2 and F 1 , D , E , F 2 . This happens when D , E , F are the feet of the perpendiculars from the vertices A , B , C to the opposite sides, so that D E F is the orthic triangle of A B C .
Note that A F = b cos A and A E = c cos A . This implies that A E F and A B C are similar, and hence that E F = a cos A . Similarly F D = b cos B and D E = c cos C . Thus we deduce that P = a cos A + b cos B + c cos C = 2 R ( sin A cos A + sin B cos B + sin C cos C ) = R ( sin 2 A + sin 2 B + sin 2 C ) where R is the radius of the circumcircle of A B C . On the other hand, the area of the triangle A B C is Δ = 2 1 R 2 ( sin 2 A + sin 2 B + sin 2 C ) = 2 1 P R In this case R = 2 5 and P = 5 6 , so that Δ = 7 0 0 .