Perfect Square in 987654321...

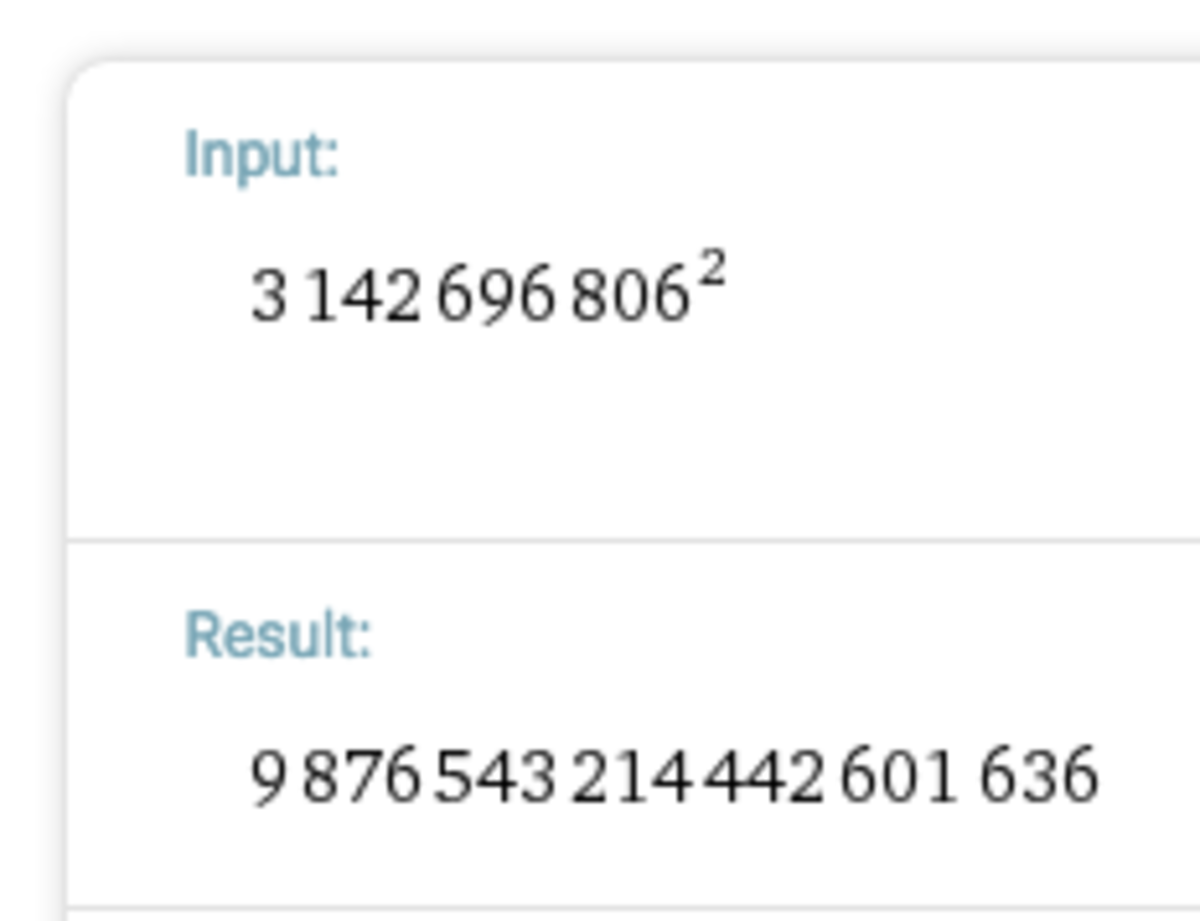
Find the smallest positive integer N such that N 2 starts with 987654321.
Note : If you use a calculator for this problem, it can be solved in under a minute. There is no need to do extensive trial and error. You could push a maximum of 100 buttons (inclusive of each digit).
The answer is 3142696806.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
Okay, this was more fun that the simpler one for 2016.
Log in to reply
And apparently a lot harder too. Just goes to show how the right interpretation of the underlying mathematics can make a seemingly difficult problem really obvious.
tq 4 the solution, sir it was clear and explanatory
The good thing about this is the answer is not always odd or even. I think there may be some generalization for determining whether n is odd/even.
Log in to reply
I'm pretty sure that 3142696806 is always odd or even.
For people who have never looked into number theory, where do 10^(n/2), 99380.799..., and 31426.968... come from?
Log in to reply
It's not "number theory" stuff per se.
It's just evaluating 9 8 7 6 5 4 3 2 1 × 1 0 n , which depends on whether n is odd or even.
When
n
is even, we get
≈
3
1
4
2
6
.
9
6
8
…
1
0
n
/
2
.
When
n
is odd, we get
≈
9
9
3
8
0
.
7
9
9
…
1
0
(
n
−
1
)
/
2
.
i used calculator. the funny thing is i got this answer 3142696806. i wanted to check if this works i squared it. the calculator was not showing the first 9 digits.
Log in to reply
Part of using a calculator is knowing it's limitations, and how one can work around it.
One approach is to use a better calculator
You miss a decimal point in the line " n odd . . . ".
I didnt get the last part could you explain what do you mean with as we vary k?
Log in to reply
We want an integer N that satisfies the conditions. When k = 1 , is there such an integer? How about k = 2 , 3 , 4 , … ? What is the smallest value of N that would result?
n odd: 9 9 3 8 0 . 7 9 9 0 0 0 6 1 1 8 … × 1 0 k ≤ N < 9 9 3 8 0 . 7 9 9 0 5 0 9 2 3 3 … × 1 0 k
- What is the smallest value of n = 2 k + 1 that will allow us to find an integer N that satisfies the above inequality?
- How can we determine it?
- What is this value of N ?
- For n = 2 1 , How many integers N will there be such that N 2 starts with 987654321?
There are only two options, since we can split 9 8 7 6 5 4 3 2 1 T in two different ways: 98'76'54'32'10'00'...'00 or 9'87'65'43'21'00'...'00.
(Fortunately, since there are three attempts to get the answer, but only two to choose from; we may do one and submit. If the former case fails, the latter will give the answer. If its do or die, do all cases first.)
In order to get the square root, consider a b c … 2 = ( A + B + C + … ) 2 = A 2 + 2 A B + B 2 + 2 A C + 2 B C + C 2 + … where A = a × 1 0 k , B = b × 1 0 k − 1 , C = c × 1 0 k − 2 , … for some k ∈ N .
Thus, N 2 = a b c … 2 = ( A 2 ) + ( 2 A + B ) ⋅ B + ( 2 ( A + B ) + C ) ⋅ C + … .
Observe that the split we made earlier corresponds to the RHS: the first term implies A = 9 (or 3); transpose the first term, then the second implies B = 9 (or 1); transpose, the second, then the third implies C = 3 (or 4); … . I'll leave the computations to you.
However the next problem would be when this seemingly infinite loop ends.
I'll demonstrate using with smaller numbers... say for 3 instead of 987654321. (I'll ignore case 30'00' … )
| N | 1 | 7 |
| N 2 | 3 | 00 |
| A F = A = 1 | 1 | |
| N 1 = N − A 2 | 2 | 00 |
| B F = 2 A + B = 2 7 | 1 | 89 |
| N 2 = N 1 − 2 nd | 11 |
Here you can count the number of trailing zeros and the number of digits of the nth term factor. Observe that 1 7 2 < N 2 < 1 8 2 = N 2 + B F + B + 1 − N 2 = 3 0 0 + 2 7 + 7 + 1 − 1 1 = 3 2 4 . The leading digit 3 is unaffected, therefore we can stop with a new N 2 = 3 2 4 and N = 1 8 .
Back to the question above, a similar scenario appears (latter case) when N 2 > 9 8 7 6 5 4 3 2 1 0 0 0 0 0 0 0 0 0 0 , and therefore, N = 3 1 4 2 6 9 6 8 0 6 .
Without calculator:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 |
|
In the same way I checked
98|76|54|32|1 |
because of the slight possibility that it would reduce the "remainders" to less than 1 more quickly.
Since the given number has nine digits, we need at least ten zeros after it so that when the asked number is squared, all the digits of the given number retain their original positions. Thus extracting the square root of 9876543210000000000, we get 3142696805.29319, the integer next to which is 3142696806
First, let's consider what it means for N 2 to have starting digits of 987654321. This simply means that
9 8 7 6 5 4 3 2 1 × 1 0 n ≤ N 2 < 9 8 7 6 5 4 3 2 2 × 1 0 n
While it's tempting to immediately take square roots, we don't really know how to deal with 1 0 2 n when n is odd. Instead, we consider the cases when n is odd / even. This gives us:
n odd: 9 9 3 8 0 . 7 9 9 0 0 0 6 1 1 8 … × 1 0 k ≤ N < 9 9 3 8 0 . 7 9 9 0 5 0 9 2 3 3 … × 1 0 k n even: 3 1 4 2 6 . 9 6 8 0 5 2 9 3 1 9 … × 1 0 k ≤ N < 3 1 4 2 6 . 9 6 8 0 6 8 4 1 8 … × 1 0 k
Now, we substitute increasing values of k till we find the smallest integer N that satisfies the inequality.
In the odd case:
When k = 0 , we get 9 9 4 8 0 . 7 9 9 0 0 0 6 1 1 8 … ≤ N < 9 9 3 8 0 . 7 9 9 0 5 0 9 2 3 3 … , which has no integer solution.
When k = 1 , we get 9 9 4 8 0 7 . 9 9 0 0 0 6 1 1 8 … ≤ N < 9 9 3 8 0 7 . 9 9 0 5 0 9 2 3 3 … , which has no integer solution.
When k = 2 , we get 9 9 4 8 0 7 9 . 9 0 0 0 6 1 1 8 … ≤ N < 9 9 3 8 0 7 9 . 9 0 5 0 9 2 3 3 … , which has no integer solution.
When k = 3 , we get 9 9 4 8 0 7 9 9 . 0 0 0 6 1 1 8 … ≤ N < 9 9 3 8 0 7 9 9 . 0 5 0 9 2 3 3 … , which has no integer solution.
When k = 4 , we get 9 9 4 8 0 7 9 9 0 . 0 0 6 1 1 8 … ≤ N < 9 9 3 8 0 7 9 9 0 . 5 0 9 2 3 3 … , which has no integer solution.
When k = 5 , we get 9 9 4 8 0 7 9 9 0 0 . 0 6 1 1 8 … ≤ N < 9 9 3 8 0 7 9 9 0 5 . 0 9 2 3 3 … , which has several integer solutions, the smallest of which is 9938079901.
In the even case:
(do the same as above)
the smallest integer N will be 3142696806. This is the answer.