Inspired by Brian Charlesworth

Geometry Level 4

( 0 , 0 , 0 ) , ( 1 , 0 , 0 ) , ( 1 , 1 , 0 ) , ( 0 , 1 , 0 ) , bottom face ( 1 , 0 , 1 ) , ( 2 , 0 , 1 ) , ( 2 , 1 , 1 ) , ( 1 , 1 , 1 ) top face \begin{array}{ l l } (0,0,0), (1,0,0), (1,1,0), (0,1,0), & \text{ bottom face} \\ (1, 0, 1 ), (2, 0, 1), (2, 1, 1), (1, 1, 1) & \text{ top face} \end{array}

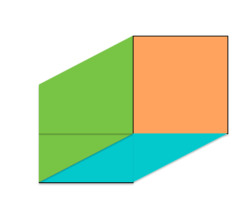
Consider a square-based prism whose vertices are given as described above. It can be considered as a tilted cube, where the top face is shifted one unit right and one unit up compared to the bottom face.

Does the south (blue) face and the west (green) face have the same surface area?

Inspiration, see reports

South face has a larger surface area Cannot be determined West face has a larger surface area Same surface area

Calvin Lin by Calvin Lin

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

1 solution

Saya Suka
Mar 27, 2021

Blue face is the floor of the slanted cube, and compared to a regular one, it didn't undergo any makeover (along with the ceiling of it). Green and it's opposite wall are now not two perpendicular walls in regards to the xy-plane anymore, but two sloped inclination of 45° (or was it 135° for the other wall?) with the same perpendicular height in comparison to any regular cube with the same base floor. Thus, with the slant height factored in (slant height > perpendicular height), West wall's surface area > South floor's surface area.

0 Helpful 0 Interesting 0 Brilliant 0 Confused

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...