Inspired by Calvin lin
x 4 − 2 x 3 + a x 2 + b x + c
If three of the roots of the polynomial above are − 5 , − 3 and 4 , find the value of a + b + c .
The answer is 361.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
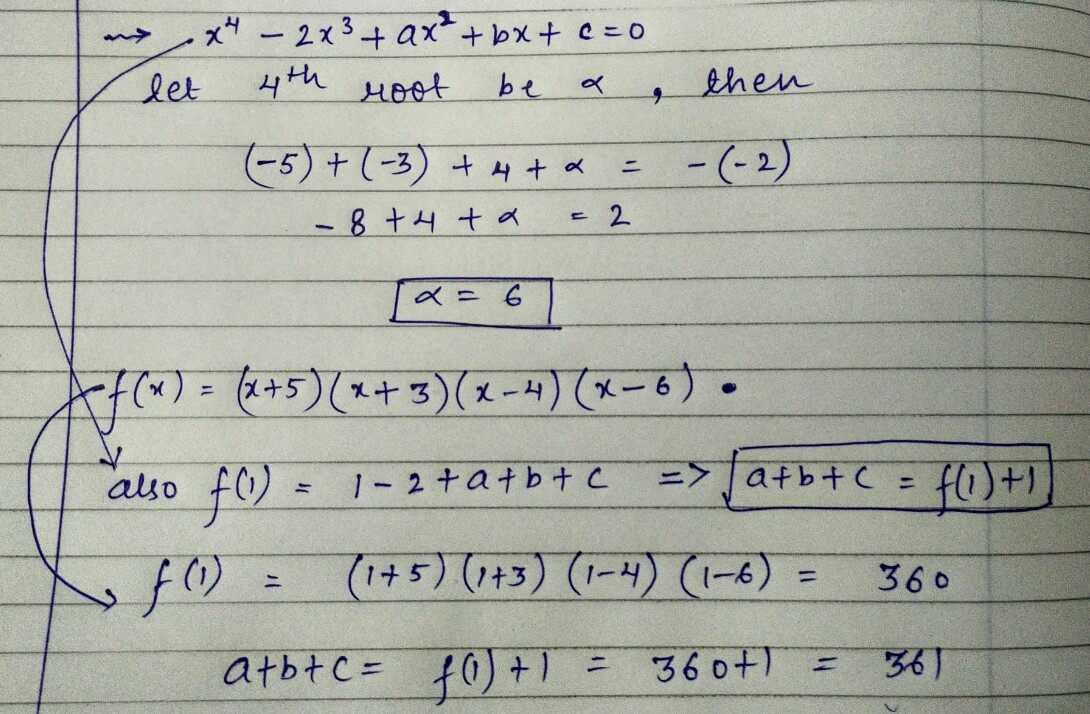
Did it the same way !!!
Your solution and handwriting both are very good
Very good solution.
Since,
−
5
,
−
3
and
4
are the roots of
x
4
−
2
x
3
+
a
x
2
+
b
x
+
c
Now putting the value of
x
=
−
5
, we get
●
6
2
5
+
2
5
0
+
2
5
a
−
5
b
+
c
=
0
=
2
5
a
−
5
b
+
c
=
−
8
7
5
.
.
.
.
.
(
1
)
Putting
x
=
−
3
●
8
1
+
5
4
+
9
a
−
3
b
+
c
=
0
=
9
a
−
3
b
+
c
=
−
1
3
5
.
.
.
.
.
.
.
.
(
2
)
Now putting,
x
=
4
●
2
5
6
−
1
2
8
+
1
6
a
+
4
b
+
c
=
0
=
1
6
a
+
4
b
+
c
=
−
1
2
8
.
.
.
.
.
.
(
3
)
Now Solving all these three equations we get,
a
=
−
4
1
b
=
4
2
c
=
3
6
0
Now,
a
+
b
+
c
=
(
−
4
1
)
+
4
2
+
3
6
0
=
3
6
1
We can use the vietas equation for finding a,b and c. Once we have got the fourth root.