Inspired by Calvin LIn and Chung Kevin

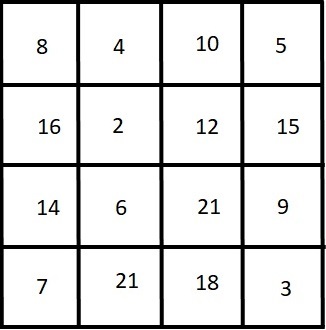
To establish an upper bound, note that we could use the first 16 positive even integers in any configuration, in which case the gcd of adjacent numbers will always exceed 1. This gives us an upper bound of $32$ for the smallest maximum. Also, we cannot include $1$ , as the gcd of it and any other positive integer will be 1. Thus at best we would be using the integers $2$ through $17$ .

However, consider what happens with primes $\ge 11$ . Each square is adjacent to at least two other squares, so any number included must have two other numbers with which it shares a non-unit gcd. With $11$ , we would have to include $22$ and $33$ at best, but as we know $32$ is an upper bound we know $11$ cannot be part of an optimal solution. The same goes for $13, 17$ and $19$ . So now the best we can do is to find a solution that involves the first 16 positive integers greater than 1 and excluding $11, 13, 17$ and $19$ . These 16 will be

$2, 3, 4, 5, 6, 7, 8, 9, 10, 12, 14, 15, 16, 18, 20, 21$ .

So if we can create a suitable grid with these 16 integers then the smallest maximum will be $\boxed{21}$ . And here is a valid solution grid:

$\Large 5 \space \space 10 \space \space 14 \space \space 7$

$\Large 20 \space \space 2 \space \space \space 6 \space \space \space 21$

$\Large 4 \space \space \space \space 8 \space \space 12 \space \space 15$

$\Large 16 \space 18 \space \space 9 \space \space \space 3$

Notes: $7$ has to be placed in a corner as it has non-unit gcd's with only $14$ and $21$ . This forces the placement of $14$ and $21$ . The remaining integers in our list that have a non-unit gcd with both $14$ and $21$ are $6,12$ and $18$ . Each of these has prime factors $2$ and $3$ only, so it makes no difference which we choose, so we'll go with $6$ . $3$ and $5$ , being primes, are trouble, so we place them in opposite corners, after which we place $9$ and $15$ adjacent to $3$ , followed by placing $10$ and $20$ adjacent to $5$ . This forces the placement of $12$ and $18$ in the remaining squares adjacent to $9$ , with the placement of $12$ also taking care of $15$ . Then we're home-free, placing the last four evens in any order in the last four squares. There are other solutions possible but this was the one that seemed most apparent.

As, Mr. Brian Charlesworth has proven that the smallest maximum integer for the grid is $\boxed{21}$ , another valid grid solution is