Inspired by toilet paper
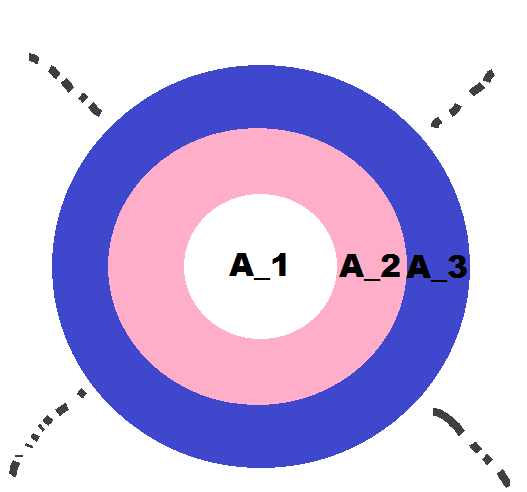
Referring to the figure above, suppose A 1 is area of first white circle, then A 2 is area of pink annulus, A 3 is area of blue annulus and like wise A n would be the annulus bounded by n th and ( n − 1 ) th circle. These n concentric circles are drawn such that the area bounded by two concentric circles remains constant, that is A 1 = A 2 = A 3 = ⋯ = A n .
Define r n to be the radius of n th circle.Evaluate r 1 r 1 0 0 correct 2 decimal places.
The answer is 10.00.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
A 1 = A 2 = A 3 = A 4 = A n U s i n g T h e o r e m o n e q u a l r a t i o s = ⇒ π r 1 2 ⇒ r 1 r n = n = π r 1 2 = π r 2 2 − π r 1 2 = π r 3 2 − π r 2 2 = π r 4 2 − π r 3 2 … … = π r n 2 − π r n − 1 2 n π r 1 2 + π r 2 2 − π r 1 2 + π r 3 2 − π r 2 2 + π r 4 2 − π r 3 2 … π r n 2 − π r n − 1 2 = n π r n 2 = n π r n 2
Putting n = 1 0 0 we have the ratio as 1 0 0 = 1 0 . 0 0 .
nihar can i know in which standard are you currently studying in because your brilliant stats are too much impressive with your age
The circular areas increase with a constant increment, and are proportional to the squares of their radii, r i 2 . Moreover, we may take r 0 = 0 . Thus the squared radius of a circle is directly proportional to its index: r i 2 ∝ i . It follows that r m r n = m n . In this case, that results in 1 0 0 / 1 = 1 0 .
Since, the area between the circles is equal,
π r n 2 − π r n − 1 2 = π r n + 1 2 − π r n 2 → 2 r n 2 = r n − 1 2 + r n + 1 2
Thus the squares of these radii form an AP.
Also ,
r 1 2 = r 2 2 − r 1 2
Thus the common difference of this AP is r 1 2
r n 2 = r 1 2 + ( n − 1 ) r 1 2
r 1 2 r n 2 = 1 + n − 1 = n
r 1 r n = n
Put n = 100 , answer = 10