Inspired by daily challenges #1

Electricity and Magnetism Level 3

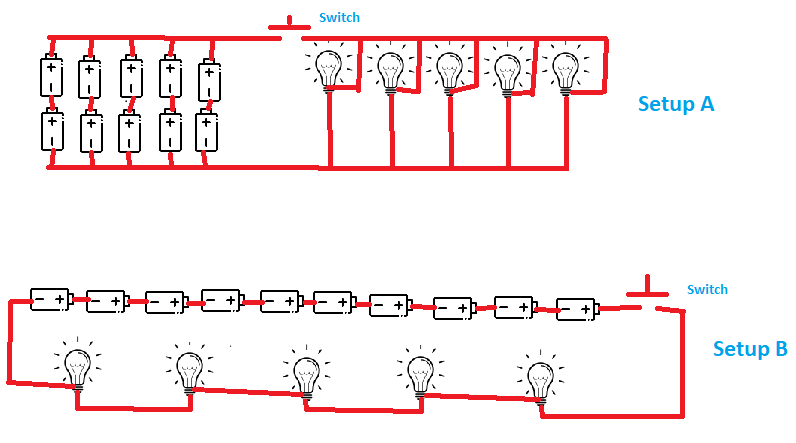
Georg is making use of 10 “D” cell batteries and 5 incandescent flashlight bulbs in a project he is designing. His project requires that he can control all 5 bulbs with a single pole switch that he has. The bulbs that he is using where intended to be used with two batteries in series. Georg has found that if he connects 3 of his batteries and one of the bulbs in series that bulb will immediately burn out when the switch is closed. Georg is considering two possible arrangements of the components in his setup which are shown in drawing above.

Which of statements given are true?

Givens and assumptions:

The batteries are all good and very similar to each other.
The bulbs are all good and very similar to each other.
All the connecting hardware (connecting point, conductors, switch, ext.) have negligible resistances.

“A” will produce the most light “A” and “B” produce the same amount of light “B” will produce the most light At least one bulb in “A” will immediately burn out At least two of the statements are true At least one bulb in “B” will immediately burn out

2 solutions

Chew-Seong Cheong
Mar 22, 2019

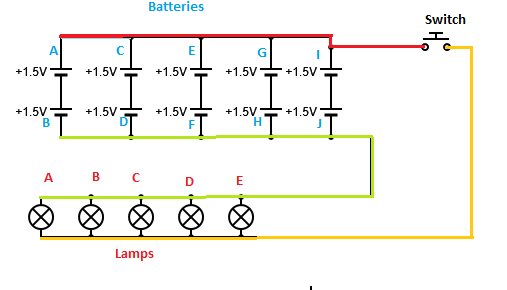
Let the voltage of a D-cell battery be $V \text{ V}$ , the resistance of a bulb be $R \ \Omega$ Then the rated current of each bulb is $I_r = \dfrac {2V}R \text{ A}$ at the rated temperature and the bulb would burn out if the current through it is $I_b = \dfrac {3V}R \text{ A} = 1.5I_r$ .

The equivalent circuit of the two setup is as shown above.

Setup A: The circuit of 5 $\times$ 2 D-cell batteries in parellel with 5 bulbs is equivalent to a 2 D-cell battery in series with a bulb. That is $V_b = 2V$ and $R_b = R$ and hence the current through the bulb is $I_b = \dfrac {V_b}{R_b} = \dfrac {2V}R = I_r < 1.5 I_r$ . So the bulb would not burn out.

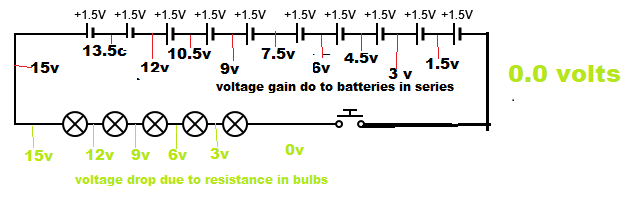
Setup B: For 10 D-cell batteries connected in series, $V_b = 10V \text{ V}$ . The 5 bulbs in series make $R_b = 5R \ \Omega$ . And hence the current through the bulb is $I_b = \dfrac {V_b}{R_b} = \dfrac {10V}{5R} = I_r < 1.5 I_r$ . So the bulb would not burn out.

We note that the 5 bulbs in Setup B have the same current as the 5 in Setup A, therefore "A" and "B" produce the same amount of light .

My statement that "at least two of the statements are true" is true if "A and B produce the same amount of light" and "at least two of the statements are true" are both True! But, not so brilliant said I was WRONG. They should rephrase the statement as "at least two of the statements above are true". That leaves no ambiguity or doubt as to weather or not the current statement is included in the statement.

John Reissner - 2 years, 2 months ago

Darryl Dennis
Mar 21, 2019

As indicated in the diagram above.

Batteries are connected in five sets of in two cell series

Example battery A and B are in series. Therefore, the red rail will be 1.5 +1.5 = 3 volts above the green rail.

When the switch is closed the yellow rail will by connected to the red rail and therefor the yellow rail will be +3 volts (above the green rail). Each of the lamps is connected directly between the yellow and the red rail. Therefore, each lamp will have a 3.0 voltage drop across its filament.

As indicated in the diagram above.

All ten Batteries are connected in a series circuit. Each battery in the series will add 1.5 volts to the output voltage. 1.5v X 10= 15 volts output from the series of batteries.

The total voltage drop across the series of 5 lamps in known to be 15 volts. Some portion of that total of 15 volts will occur in each of the bulbs proportional to the resistance within the individual bulbs. All of the bulbs are similar and therefor their resistance can be assumed to also be similar. 15V/5 bulbs = 3v/bulb voltage drop.

Each bulb in both the setups have a 3v voltage drop. 3.0 volts is the intended voltage for these bulbs, therefor none of the bulbs would be subjected to a higher current do to a high voltage drop in the filament. No bulbs are in danger of burning out from high current flow. At each bulb there is a 3v drop across the same value of resistance applying power W=V^2 / R we can determine the energy being consumed (resulting in heat and light) is the same value for all the bulbs.

All the bulbs have the same light output.

Inspired by daily challenges #1

2 solutions

0 pending reports