Inspired by daily challenges #2
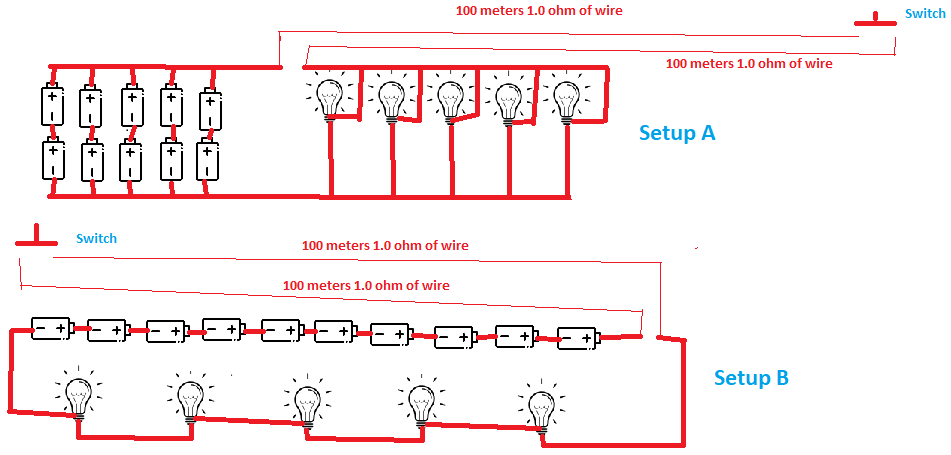
Georg is making use of 10 “D” cell batteries and 5 incandescent flashlight bulbs in a project he is designing. His project requires that he can control all 5 bulbs with a single pole switch that he has installed at a location that is 100 meters from the project setup. Georg has two lengths of small gauge wire that he is using to connect his project to his control switch. George has measured the resistance of his lengths of wire to be 1.0 ohm for each of the 100-meter lengths he intends to use. He also measured the resistance of one of his bulbs to be 1.0 ohm when the bulb is at room temperature (not lit). The bulbs that he is using where intended to be used with two batteries in series. Georg has found that if he connects 3 of his batteries and one of the bulbs in series that bulb will immediately burn out when the switch is closed.
Georg is considering two possible arrangements of the components in his setup which are shown in drawing above.
Which of statements given are true?
Givens and assumptions:
- The batteries are all good and very similar to each other.
- The bulbs are all good and very similar to each other.
- Other than the long wires the connecting hardware (connecting point, conductors, switch, ext.) have negligible resistances.
- The resistance of the bulb’s filaments will not change with temperature (not realistic but greatly simplifies this solution while not effecting the overall principles of the solution)
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
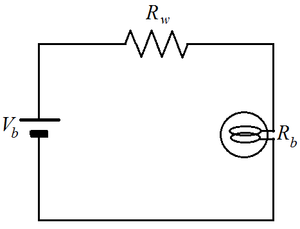
Let the voltage of a D-cell battery be V V . Since the resistance of a bulb is 1 Ω Then the rated current of each bulb is 1 2 V = 2 V A and the bulb would burn out if the current through it is I b = 3 V A .
The equivalent circuit of the two setup is as shown above.
Setup A: The 5 × 2 D-cell batteries in parallel give a V b = 2 V V . The 2 × 100-m wires in series make R w = 2 Ω . The 5 bulbs in parallel make R b = 5 1 = 0 . 2 Ω . The current through the circuit I = R w + R b V b = 2 . 2 2 V = 1 1 1 0 V . The current through each bulb I b = 5 I = 1 1 2 V < 3 V . So the bulb would not burn out.
Setup B: For 10 D-cell batteries connected in series, V b = 1 0 V V . The 2 × 100-m wires in series make R w = 2 Ω . The 5 bulbs in series make R b = 5 Ω . The current through the circuit I = R w + R b V b = 7 1 0 V . The current through each bulb I b = I = 7 1 0 V < 3 V . So the bulb would not burn out.
We note that the 5 bulbs in Setup B have a higher current than the 5 in Setup A, therefore "B" produces more light .
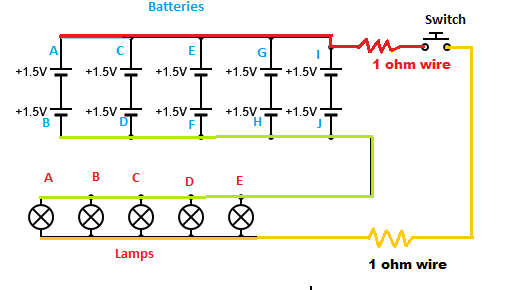 As indicated in the diagram.
As indicated in the diagram.
Batteries are connected in five sets of in two cell series
Example battery A and B are in series. Therefore, the red rail will be 1.5 +1.5 = 3 volts above the green rail. The battery supply voltage is 3.0volts.
The five lamps are in a parallel arrangement and are in series with two wire resistances. Calculating the resulting resistance of the lamp/wire arrangement. R A 1 + R B 1 + R C 1 + R D 1 + R E 1 = R l a m p s 1 R l a m p s = 5 1 = 0 . 2 o h m s R t o t a l = R l a m p s + R w i r e 1 + R w i r e 2 R t o t a l = 0 . 2 + 1 + 1 = 2 . 2 o h m s
calculate the total current that the batteries are supplying.
I = R V = 2 . 2 3 = 1 . 3 6 a m p s
calculate voltage drop in the long small gauge wires V = I R calculate the voltage that is across the lamps after the line loss do to very high wire resistance to the switch
V l a m p s = V t o t a l − V w i r e − V w i r e V l a m p s = 3 − 1 . 3 6 − 1 . 3 6 = 0 . 2 8 v o l t s
clearly this is not a good circuit to control the bulbs for 100 meters with this small gauge wires. Total power used by each bulb can be calculated to show how little power is used to possibly make light.
W l a m p = V 2 / R = 1 0 . 2 8 2 = 0 . 0 7 8 W a t t s / b u l b
There would be no light at all from any of the lamps, most of the battery energy is going to heat the long switch wires.
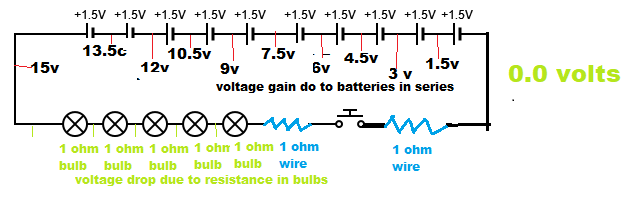 As indicated in the diagram.
As indicated in the diagram.
All ten Batteries are connected in a series circuit. Each battery in the series will add 1.5 volts to the output voltage. 1.5v X 10= 15 volts output from the series of batteries.
All five of the bulbs and the two connecting wire are in a series circuit. calculate the total resistance of that circuit.
R t o t a l = R l a m p s + R w i r e s = 5 + 1 + 1 = 7 o h m s
calculate current supplied by batteries.
I = R V = 7 1 5 = 2 . 1 4 a m p s
Calculate the voltage drop across each of the bulbs. by applying ohms law. Find the the lamp voltage drop using the current through lamp, the lamps resistance
V
d
r
o
p
=
2
.
1
4
A
∗
1
Ω
=
2
.
1
4
v
calculate the total power used by each bulb to determine how much energy there may be to produce light.
W l a m p = V 2 / R = 1 2 . 1 4 2 = 4 . 5 8 W a t t s / b u l b
much more of the total power produced by the batteries is delivered to the lamps . But still not good.
calculate the energy the each lamp would receive if the long switch wires where not in use.
W l a m p = V 2 / R 1 Ω 3 A 2 = 9 . 0 W a t t s / b u l b
~ 50% less power per bulb do to line loss on his switch wires, perhaps Georg should consider using larger gauge wires to his switch.
In the previous problem, none of the bulbs were in danger of burning out, and the introduction of resistance makes them even less likely to burn out in this case.
In Setup B, the 5 ohms of series bulb resistance still takes most of the total voltage since it is larger than the 2 ohm switch resistance. So Setup B still functions similarly to before, but with the bulbs a bit dimmer.
In the previous problem, each bulb in Setup A had twice the battery voltage across it. Now, each bulb in Setup A has dramatically less voltage, due to the voltage divider between the 2 ohm switch resistance and the equivalent 0.2 ohm parallel set of bulbs.
So the brightness of Setup A is dramatically reduced relative to the previous problem, while the brightness of Setup B is only moderately reduced.
A nice quantitative followup problem to this would be to ask for the ratio of the Setup A total bulb power to the Setup B total bulb power.