Inspired by Dish-washing!

Consider the following diagram-

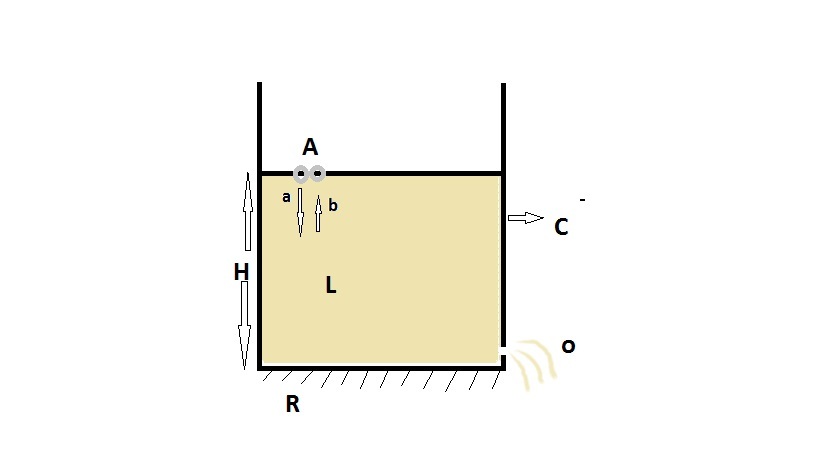
L is a murky ideal liquid of refractive index $n=2.23$ filled in a container C of cross section Z to a height of H = 64cm. Container C has an orifice O (near the bottom) of cross section z from which the liquid flows out starting at a time t = 0. L has a unique property that the intensity of light transmitted through it varies as $I=I_{initial}e^{-10d}$ where d is the distance travelled by light through the the liquid.The bottom R of C is reflecting (perfectly). A (of mass 50g) consists of a floating light emitter (it emits a narrow beam of light) a and receiver b which lie very close to each other. a emits light of intensity $I_{0}$ and $b$ responds only when it receives light of intensity greater than $0.04076I_{0}$ . If t (to the nearest positive integer) is the time after which b responds and if U is the loss in potential energy of A in the time interval between the emission of the light ray which produces the first response and the reception of the same such that $U=m10^{-x}$ ,

find |t| + x.

Given: - $\frac{z}{Z} =10^{-4}$

• $c= 3 \times 10^{8}ms^{-1}$

• $g= 10ms^{-2}$