Inspired by Ethan
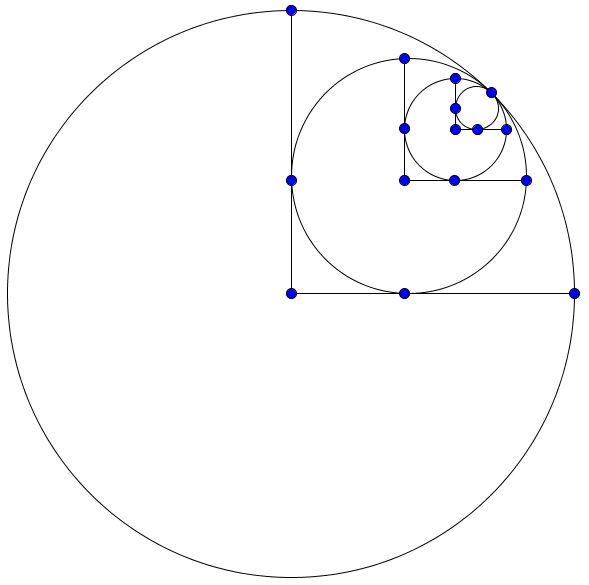 If the pattern of inscribed
circles
shown in the image above is repeated infinitely, each new circle is inscribed within a quadrant of the larger circle and the
radius
of the largest circle is 10, then what is the area of all the circles?
If the pattern of inscribed
circles
shown in the image above is repeated infinitely, each new circle is inscribed within a quadrant of the larger circle and the
radius
of the largest circle is 10, then what is the area of all the circles?
The area of all the circles can be expressed as a π ( b + c ) , where a , b and c are integers with b square-free. Find a + b + c .
The answer is 53.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
Perfect solution. This also explains how you got the relationship between the two radii. Great work!
I rarely find solutions this detailed. Upvote!
Log in to reply
Thanks. I personally feel that the most important part is showing how to find the radius of the smaller circles, since this is a geometry question
I'm glad I'm not the only one who struggles at drawing circles ;)
Let the largest radius be r 0 = 1 0 , the next largest be r 1 , then r 2 and so on. Then we note that:
r 0 ⟹ r 1 r 2 r 3 . . . ⟹ r k = r 1 + 2 r 1 = 1 + 2 r 0 = ( 1 + 2 ) 2 r 0 = ( 1 + 2 ) 3 r 0 . . . = ( 1 + 2 ) k r 0
The area of all the circles is given by:
A = k = 0 ∑ ∞ π r k 2 = π r 0 2 k = 0 ∑ ∞ ( 1 + 2 1 ) 2 k = π r 0 2 k = 0 ∑ ∞ ( 3 + 2 2 1 ) k = π r 0 2 ( 1 − 3 + 2 2 1 1 ) = 1 0 0 π ( 2 + 2 2 3 + 2 2 ) = 5 0 π ( 1 + 2 3 + 2 2 ) = 5 0 π ( ( 1 + 2 ) ( 2 − 1 ) ( 3 + 2 2 ) ( 2 − 1 ) ) = 5 0 π ( 1 + 2 )
⟹ a + b + c = 5 0 + 2 + 1 = 5 3
The relation between radius of bigger circle ( x ) and and radius of circle inscribed ( r ) is: r = 1 + 2 x .
Radius of first circle= 1 0 [ Given ]
Radius of next circle= 1 + 2 1 0
Radius of next circle= 1 + 2 1 + 2 1 0 = ( 1 + 2 ) 2 1 0
⋅ ⋅ ⋅ ⋅ ⋅ ⋅
As we know area of circle is: π r 2
Area of all circles: ⇒ π ( 1 0 ) 2 + π ( 1 + 2 1 0 ) 2 + π ( ( 1 + 2 ) 2 1 0 ) 2 + π ( ( 1 + 2 ) 4 1 0 ) 2 + ⋅ ⋅ ⋅ ⋅
⟹ π [ 1 0 0 + 1 0 0 ( ( 1 + 2 ) 2 1 + ( 1 + 2 ) 4 1 + ( 1 + 2 ) 6 1 + ⋅ ⋅ ⋅ ⋅ ) ]
Using Geometric progression.
⟹ π [ 1 0 0 + 1 0 0 ( ( 1 + 2 ) 2 − 1 1 ) ]
⟹ π [ 1 0 0 + 1 0 0 ( 2 2 + 2 1 ) ]
⟹ π [ 1 0 0 + 5 0 ( 2 − 1 ) ]
⟹ 5 0 π ( 1 + 2 )
∴ a + b + c = 5 0 + 2 + 1 = 5 3
@Abhay Kumar You only showed how to calculate the final answer. I urge you to show your working.
Log in to reply
Done.Is it ok? :-)
Log in to reply
I wanted you to show how you ended up getting the relationship of the radii of the two circles, which makes the solution complete. You could refer Hung Woei Neoh's solution.

Let us analyze the first two circles:
For easy naming, let us call the circles c 1 , c 2 , c 3 , … . The radius of these circles will be r 1 , r 2 , r 3 , … and the area of these circles will be a 1 , a 2 , a 3 , …
First of all, since O B Q D is a quadrant, we know that ∠ A O C = 9 0 ∘ . Lines O C D and O A B are tangent to c 2 , so we also know that ∠ O C P = ∠ O A P = ∠ A P C = 9 0 ∘ . We know that A P = C P = r 2 , therefore it is obvious that O A P C is a square. With this, we can find O P .
O P = C P 2 + A P 2 = r 2 2 + r 2 2 = 2 r 2 2 = 2 r 2
Note that P Q = r 2 and O Q = r 1 = 1 0 . We can then say that
O Q = O P + P Q r 1 = 2 r 2 + r 2 r 2 = 2 + 1 r 1 = 2 + 1 1 0
Now, notice that for the circles c 2 and c 3 , c 3 and c 4 ...., the pattern repeats in the exact same manner.
This implies that r n + 1 = 2 + 1 r n
The radius of the circles, r 1 , r 2 , r 3 , r 4 , … are 1 0 , 2 + 1 1 0 , ( 2 + 1 ) 2 1 0 , ( 2 + 1 ) 3 1 0 , …
The areas of the circles, a 1 , a 2 , a 3 , a 4 , … are (use a = π r 2 ): 1 0 0 π , ( 2 + 1 ) 2 1 0 0 π , ( 2 + 1 ) 4 1 0 0 π , ( 2 + 1 ) 6 1 0 0 π , …
Notice that the areas of these circles form a geometric progression where a = 1 0 0 π and r = ( 2 + 1 ) 2 1
Now, we are looking for the sum of the areas of all the circles when this pattern is repeated infinitely. In other words, the sum of the GP above when n = ∞ . Use the formula S ∞ = 1 − r a :
A = a 1 + a 2 + a 3 + a 4 + … = 1 − ( 2 + 1 ) 2 1 1 0 0 π = 1 − 3 + 2 2 1 1 0 0 π = 3 + 2 2 3 + 2 2 − 1 1 0 0 π = 2 + 2 2 1 0 0 π ( 3 + 2 2 ) = 2 ( 2 + 1 ) ( 2 − 1 ) 1 0 0 π ( 3 + 2 2 ) ( 2 − 1 ) = 2 − 1 5 0 π ( 3 2 + 4 − 3 − 2 2 ) = 5 0 π ( 2 + 1 )
⟹ a = 5 0 , b = 2 , c = 1 , a + b + c = 5 0 + 2 + 1 = 5 3