Raising A Pyramid

Geometry Level 4

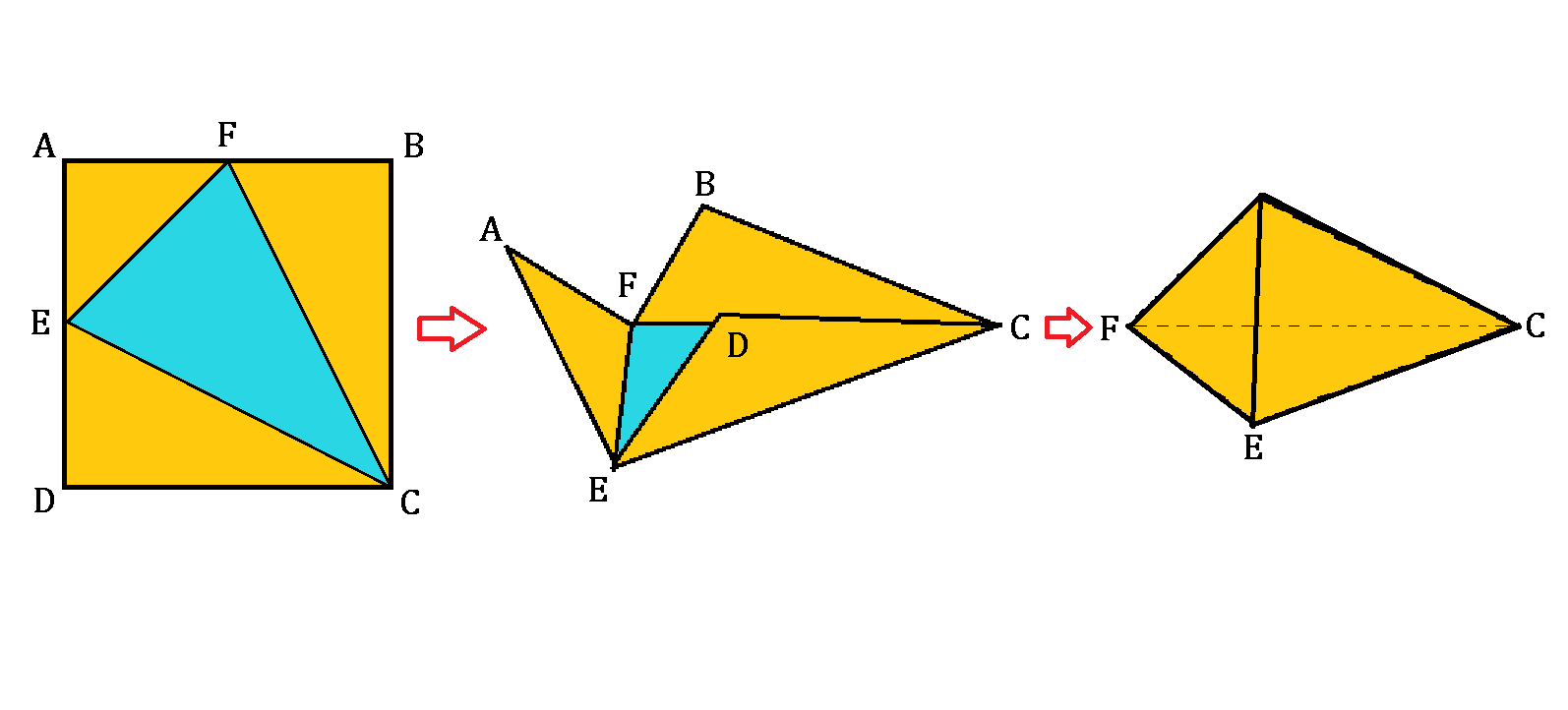
A square $ABCD$ has points $E$ and $F$ as its midpoints on $AD$ and $AB$ , respectively. The square is then folded such that the vertices $A$ , $B$ , and $D$ joined together become a new vertex of the pyramid with triangular base $EFC$ .

If the square has a side length of $6\text{ cm}$ , what is the volume of the pyramid (in $\text{cm}^3$ )?

Inspiration .

The answer is 9.

1 solution

Worranat Pakornrat
Sep 2, 2016

Relevant wiki: Volume of a Pyramid

If we denote the vertex of the pyramid as point $V$ , then at this point, there are $3$ right angles joining as if it were the corner of a cuboid. Hence, we can flip the pyramid to let it lie on the triangular base $VEF$ as shown below:

Then if we visualize a triangular-based prism with the same height as the pyramid, it is clear that the volume of the pyramid will be $\dfrac{1}{3}$ of the prism as a general formula for pyramidal volume.

And at this perspective, the base $b$ is the right triangle $VEF$ and the height $h$ is $VC$ .

Clearly, $VC = BC = 6$ , and $VE = VF = AF = 3$ .

Thus, volume of the pyramid = $\dfrac{1}{3}\times b\times h = \dfrac{1}{3} \times (\dfrac{1}{2}\times 3 \times 3)\times 6 = \boxed{9}$ .

As a result, the pyramid will have the volume of $\boxed{9}$ .

How do you find this so easy I am so frustrated I can't do anything at all lol.

Rico Lee - 4 years, 8 months ago

@WorranatPakornrat Can you prove how your stated factoid is true i.e, the volume of the given pyramid is one thirds of a triangular prism diagrammatically. I used paper origami but it couldn't prove it to be true.

Aniruddha Bagchi - 4 years, 5 months ago

To join points $A, B, C$ as vertex $V$ , $AF = AE = VE = VF$ . So $VEF$ is a right-angled isosceles triangle or literally half a square. The only way we can conjoint three right-angled faces is to create a corner of the cuboid or specifically if $V$ is the point of origin in 3D planes, vectors $VC, VE, VF$ would be along $x, y, z$ axes. Thus, such shape is a pyramid with half-square base or literally one-sixth of cuboid or one-third of half-square based prism.

Worranat Pakornrat - 4 years, 5 months ago

Raising A Pyramid

The answer is 9.

1 solution

0 pending reports