Where's The Borderline?
How many integers from 1 to 10000 (both inclusive) can be written as
⌊ 2 x ⌋ ⌊ 3 x ⌋
for some real number x ?
The answer is 202.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
Hey hey. A fan. hmmmm.
Let i ( x ) = ⌊ 2 x ⌋ ⌊ 3 x ⌋ . Consider n ≤ x < n + 1 , where n is an integer, then there are 4 integers i ( x ) generated (see figure below).
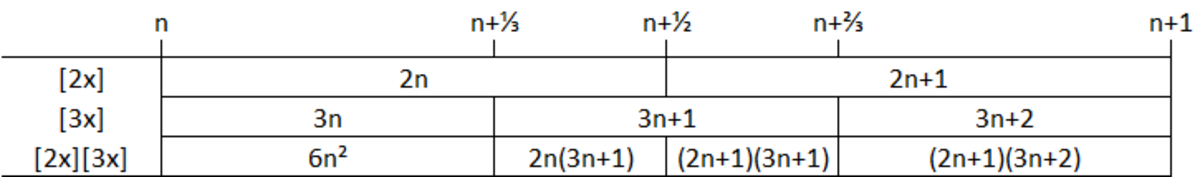
i ( x ) = ⎩ ⎪ ⎪ ⎪ ⎨ ⎪ ⎪ ⎪ ⎧ 6 n 2 2 n ( 3 n + 1 ) ( 2 n + 1 ) ( 3 n + 1 ) ( 2 n + 1 ) ( 3 n + 2 ) n ≤ x < n + 3 1 n + 3 1 ≤ x < n + 2 1 n + 2 1 ≤ x < n + 3 2 n + 3 2 ≤ x < n + 1
This is true for x < 0 . To only consider non-negative n , we do the following:
⎩ ⎪ ⎪ ⎪ ⎨ ⎪ ⎪ ⎪ ⎧ 6 m 2 2 m ( 3 m + 1 ) ( 2 m + 1 ) ( 3 m + 1 ) ( 2 m + 1 ) ( 3 m + 2 )
⇒ ⎩ ⎪ ⎪ ⎪ ⎨ ⎪ ⎪ ⎪ ⎧ 6 ( − m ) 2 ( − 2 m ) [ − ( 3 m − 1 ) ] [ − ( 2 m − 1 ) ] [ − ( 3 m − 1 ) ] [ − ( 2 m − 1 ) ] [ − ( 3 m − 2 ) ] = 6 ( m ) 2 = 2 m ( 3 m − 1 ) = ( 2 m − 1 ) ( 3 m − 1 ) = ( 2 m − 1 ) ( 3 m − 2 )
Replace m = n + 1 , we have:
⇒ ⎩ ⎪ ⎪ ⎪ ⎨ ⎪ ⎪ ⎪ ⎧ 6 ( m ) 2 2 m ( 3 m − 1 ) ( 2 m − 1 ) ( 3 m − 1 ) ( 2 m − 1 ) ( 3 m − 2 ) = 6 ( n + 1 ) 2 = 2 ( n + 1 ) ( 3 n + 2 ) = ( 2 n + 1 ) ( 3 n + 2 ) = ( 2 n + 1 ) ( 3 n + 1 )
We note that negative n introduce an extra i ( x ) = 2 ( n + 1 ) ( 3 n + 2 ) . Therefore, for each positive n we have five i ( x ) as follows:
i ( n ) = ⎩ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎨ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎧ 6 n 2 2 n ( 3 n + 1 ) ( 2 n + 1 ) ( 3 n + 1 ) ( 2 n + 1 ) ( 3 n + 2 ) 2 ( n + 1 ) ( 3 n + 2 ) and i ( 0 ) = ⎩ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎨ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎧ 0 0 1 2 4
For i ( n ) ≥ 1 0 0 0 0 , we have:
2 ( n + 1 ) ( 3 n + 2 ) ≥ 1 0 0 0 0 ⇒ ( n + 1 ) ( 3 n + 2 ) ≥ 5 0 0 0
⇒ 3 n 2 + 5 n − 4 9 9 8 ≥ 0 ⇒ n ≥ 3 9 . 9 9
And we note that: i ( 4 0 ) = ⎩ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎨ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎧ 9 6 0 0 9 6 8 0 9 8 0 1 9 8 8 2 1 0 0 0 4
Therefore, the number of integers from 1 to 1 0 0 0 0 can be written as ⌊ 2 x ⌋ ⌊ 3 x ⌋ is:
N = 4 1 × 5 − 3 = 2 0 2
I was somewhat there till your replacement of m=n+1 but after that don't know WHAT happened .😕😕
I have a (somewhat inefficient but still very fast) Java solution. It is based on the fact that since we are only looking for values between 1 and 10,000,
−
4
1
<
x
<
4
1
.
Link 1
Link 2 (if Link 1 doesn't work)
EDIT: the increment I use to check for new values of n is
Δ
x
=
0
.
0
1
, but there is a much greater value of
Δ
x
that still guarantees the correct answer. I wonder what it is?
It's nice to see a computer science solution !
As shown by Chew-Seong Cheong, the function changes value at n , n + 6 2 , n + 6 3 , n + 6 4 , and n + 1 , so the maximum value of Δ x can be 6 1
PROGRAM Floor 2x and _3x; {202 = 40 + 122 + 40. 1 tenth. Flexible for each check.}
USES CRT;
VAR i, count: LONGINT; n, x: EXTENDED; num, num1, num2: ARRAY[1..10001] OF WORD; Skip: BOOLEAN;
FUNCTION Flr(x: EXTENDED): LONGINT; BEGIN IF x<0.0 THEN Flr:=TRUNC(x)-1 ELSE Flr:=TRUNC(x) END;
FUNCTION Dmp(x: EXTENDED): LONGINT; BEGIN IF x>10000.0 THEN Dmp:=10001 ELSE Dmp:=TRUNC(x) END;
BEGIN CLRSCR;
FOR i:=1 TO 10001 DO
Num1[i]:=i;
FOR i:=1 TO 10001 DO
Num2[i]:=i;
WRITELN('Fine verification to tenth requires about 0.6 seconds...');
n:=0.0;
REPEAT
x:=0.1*n;
Num1[Dmp(1.0*Flr(2.0*x)*Flr(3.0*x))]:=0;
Num2[Dmp(1.0*Flr(-2.0*x)*Flr(-3.0*x))]:=0;
n:=n+1.0
UNTIL n>100000.0;
CLRSCR;
WRITELN('Verification completed. Do you want to see one by one for counts?');
WRITE('If NO then press [N] else press [ENTER] to read> ');
IF UPCASE(READKEY)='N' THEN
Skip:=TRUE
ELSE
Skip:=FALSE;
WRITELN;
FOR i:=1 TO 10001 DO
Num[i]:=i;
count:=0;
FOR i:=1 TO 10000 DO
IF (Num1[i]=0) OR (Num2[i]=0) THEN {Can be changed to count for others.}
BEGIN
INC(count);
IF NOT Skip THEN
BEGIN
WRITELN(Num[i]:4, '; Count = ', count);
IF READKEY=#27 THEN
Skip:=TRUE
END
ELSE
WRITELN(Num[i]:4, '; Count = ', count)
END;
WRITELN;
WRITE('Total counts = ', count, ' ', 'Press [Esc] to quit> ');
REPEAT UNTIL READKEY=#27
END.

Relevant wiki: Floor and Ceiling Functions - Problem Solving
Let f ( x ) = ⌊ 2 x ⌋ ⌊ 3 x ⌋
Important Fact: ⌊ x ⌋ is a function that remains constant, and only changes its value (increases by 1) when x crosses an integer, say n .
Therefore ⌊ 2 x ⌋ increases when x crosses 2 n and ⌊ 3 x ⌋ increases when x crosses 3 n .
⌊ 2 x ⌋ ⌊ 3 x ⌋ will increase when x crosses 6 n .
Another important fact: The floor function is neither odd nor even, so we need to take two cases separately : x is non-negative, and x is negative.
Case 1: x is non-negative
Note that when x is an integer n , f will be equal to 6 n 2 . So all numbers of the form 6 n 2 can be written in this form.
Now let's see how the value of f changes as x varies from n to n + 1 . Since the period of f is lcm ( 2 1 , 3 1 ) = 1 , we can be sure that the same pattern will be followed as x goes from n + 1 to n + 2 .
As we saw above, f only changes when x crosses and integral multiple of 6 1 , we can divide the interval [ n , n + 1 ) into 6 equal intervals.
Interval [ n , n + 6 1 ) [ n + 6 1 , n + 6 2 ) [ n + 6 2 , n + 6 3 ) [ n + 6 3 , n + 6 4 ) [ n + 6 4 , n + 6 5 ) [ n + 6 5 , n + 1 ) ⌊ 2 x ⌋ 2 n 2 n 2 n 2 n + 1 2 n + 1 2 n + 1 ⌊ 3 x ⌋ 3 n 3 n 3 n + 1 3 n + 1 3 n + 2 3 n + 2 f ( x ) 6 n 2 6 n 2 6 n 2 + 2 n 6 n 2 + 5 n + 1 6 n 2 + 7 n + 2 6 n 2 + 7 n + 2
We see that there are 4 distinct values that f takes as x goes from n to n + 1 viz. 6 n 2 , 6 n 2 + 2 n , 6 n 2 + 5 n + 1 , 6 n 2 + 7 n + 2 .
When n = 0 , we only get two values - 1 , 2 since we don't want 0. For all n > 0 , we get 4 values, for example for n = 1 , we get 6 , 8 , 1 2 and 1 5 . These are the numbers that can be written in the desired form. If we arrange them in ascending order, it is not hard to prove that f ( n ) = 6 n 2 will be the ( 4 n − 1 ) th term in the sequence.
1 is the minimum number in the range of f . To find the maximum number less than 1 0 0 0 0 , the easiest way would be to find the greatest possible n , by setting 6 n 2 ≤ 1 0 0 0 0 .
⟹ n 2 ≤ 1 6 6 6
⟹ n ≤ 4 0
The maximum n is 4 0 .
Now we check if f ( 4 0 + 6 5 ) < 1 0 0 0 0 .
f ( 4 0 + 6 5 ) = 6 × 4 0 2 + 7 × 4 0 + 2 = 9 8 8 2 ≤ 1 0 0 0 0 which works as well.
We know that f ( 4 0 ) = 6 × 4 0 2 = 9 6 0 0 is the ( 4 × 4 0 − 1 ) th term, ie 1 5 9 th term. Therefore 9 8 8 2 will be the 1 5 9 + 3 = 1 6 2 th term.
However, we mustn't forget Case 2, in which x is negative.
Case 2: x is negative.
For some negative integer k , let m = k − 2 1 . The motivation to do this will become clear shortly. Now let's see how f varies as x goes from m to m + 1 .
Interval [ m + 6 5 , m ) [ m + 6 4 , m + 6 5 ) [ m + 6 3 , m + 6 4 ) [ m + 6 2 , m + 6 3 ) [ m + 6 1 , m + 6 2 ) [ m , m + 6 1 ) ⌊ 2 x ⌋ 2 k 2 k 2 k 2 k − 1 2 k − 1 2 k − 1 ⌊ 3 x ⌋ 3 k + 1 3 k 3 k 3 k − 1 3 k − 1 3 k − 2 f ( x ) 6 k 2 + 2 k 6 k 2 6 k 2 6 k 2 − 5 k + 1 6 k 2 − 7 k + 2 6 k 2 − 7 k + 2
Since k is a negative number, we can replace it by − n , where n is a positive number. Observe for each n , the outputs are now 6 n 2 − 2 n , 6 n 2 , 6 n 2 + 5 n + 1 , 6 n 2 + 7 n + 2 .
That is, for each n , f ( − n ) has exactly one element in its range ( 6 n 2 − 2 n ) which is not present in range of f ( n ) , ie a one-to-one correspondence. Since we calculated n to be 4 0 in the previous case, there will be 4 0 more numbers which can be written in this form if x is negative.
There are 1 6 2 + 4 0 = 2 0 2 integers from 1 to 1 0 0 0 0 which can be written as ⌊ 2 x ⌋ ⌊ 3 x ⌋ □ .