Inspired by Neel Khare

Algebra Level 3

What is the domain of

log ⁡ x + 1 x + 2 ? \log \frac{x+1}{x+2} ?

Inspiration

x > − 2 x > -2 x > − 1 x > -1 x > − 1 and x < − 2 x > -1 \text{ and } x < -2 x > 0 x > 0

Calvin Lin by Calvin Lin

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

2 solutions

Zee Ell
Oct 26, 2016

Since the domain of log(y) is y > 0 , therefore:

x + 1 x + 2 > 0 \frac {x+1}{x+2} > 0

1 − 1 x + 2 > 0 1 - \frac {1}{x+2} > 0

1 > 1 x + 2 1 > \frac {1}{x+2}

Now, we have two cases:

Case I : x + 2 > 0 ⟺ x > − 2 \text {Case I : } x + 2 > 0 \iff x > -2

1 > 1 x + 2 ⟺ x + 2 > 1 ⟺ x > − 1 1 > \frac {1}{x+2} \iff x + 2 > 1 \iff x > -1

As x > -1 > -2 in this case, therefore the relevant interval is x > -1 here.

Case II : x + 2 < 0 ⟺ x < − 2 \text {Case II : } x + 2 < 0 \iff x < -2

Since multiplying by a negative number changes the direction of the inequality sign to the opposite:

1 > 1 x + 2 ⟺ x + 2 < 1 ⟺ x < − 1 1 > \frac {1}{x+2} \iff x + 2 < 1 \iff x < -1

As x < -2 < -1 in this case, therefore the relevant interval is x < -2 here.

Hence, the domain of the function is:

x > − 1 and x < − 2 \boxed {x > -1 \text { and } x < -2}

2 Helpful 0 Interesting 0 Brilliant 0 Confused

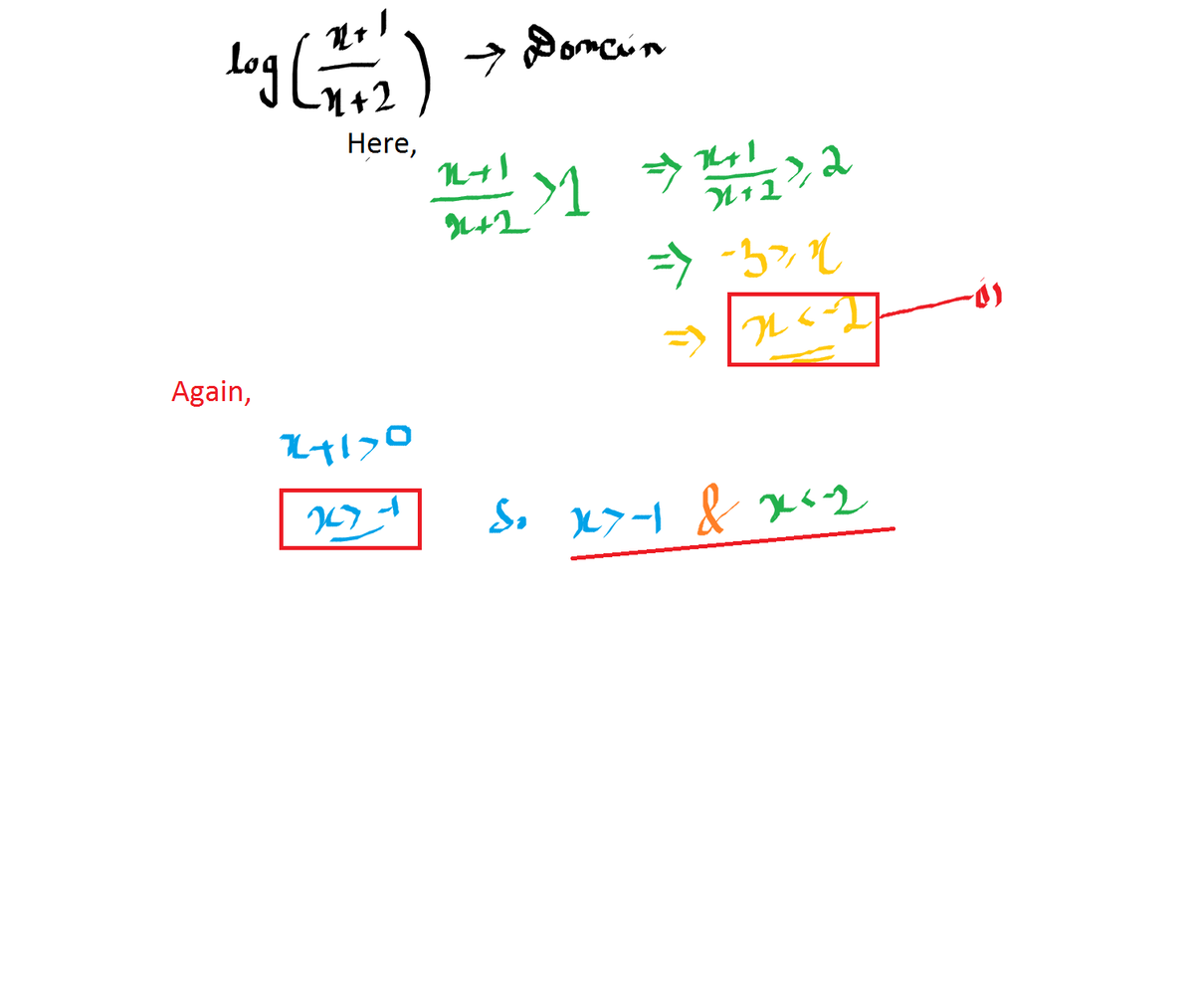
Great! It's a common misconception that the domain of log ⁡ f ( x ) g ( x ) \log \frac{ f(x) } { g(x) } is either x > 0 x > 0 or f ( x ) > 0 f(x) > 0 . What we need is for the entire expression to be positive.

A much easier way to deal with these rational inequalities is to multiply throughout by the square of the denominator to ensure positivity. This way,

x + 1 x + 2 > 0 ⇔ ( x + 1 ) ( x + 2 ) > 0 \frac{x+1}{x+2} > 0 \Leftrightarrow (x+1)(x+2) > 0

and the rest follows.

Calvin Lin Staff - 4 years, 7 months ago
Md Zuhair
Oct 26, 2016

0 Helpful 0 Interesting 1 Brilliant 0 Confused

Thanks for submitting a solution. Unfortunately, this solution has numerous issues.

  1. Where did the condition that x + 1 x + 2 > 1 \frac{x+1}{x+2} > 1 come form?
  2. Is it true that if x + 1 x + 2 > 1 \frac{x+1}{x+2} >1 then x + 1 x + 2 ≥ 2 \frac{ x+1}{x+2} \geq 2 ? If so, what happens for x = 100 x = 100 ?
  3. Are you sure that x + 1 x + 2 ≥ 2 ⇔ x + 1 ≥ 2 ( x + 2 ) \frac{x+1}{x+2} \geq 2 \Leftrightarrow x+1 \geq 2 (x+2) ?
  4. Is it true that if − 3 ≥ x ⇔ x < − 2 -3 \geq x \Leftrightarrow x < -2 ?
  5. Review sat inequalities

Calvin Lin Staff - 4 years, 7 months ago

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...