Inspired by Nihar Mahajan
Given a rectangle of dimensions 6 × 4 , E is a point on side A B such that A E = 2 E B , F is the mid point of side B C , Than find out the area of quadrilateral P Q R S
The answer is 0.8.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
i did exactly the same way u did, I think u should correct from ( P = 2 , 4 , 2 , 4 ) to ( P = 2 . 4 , 2 . 4 )
thanks!!! :-) :-)
Log in to reply
The solution has been edited.
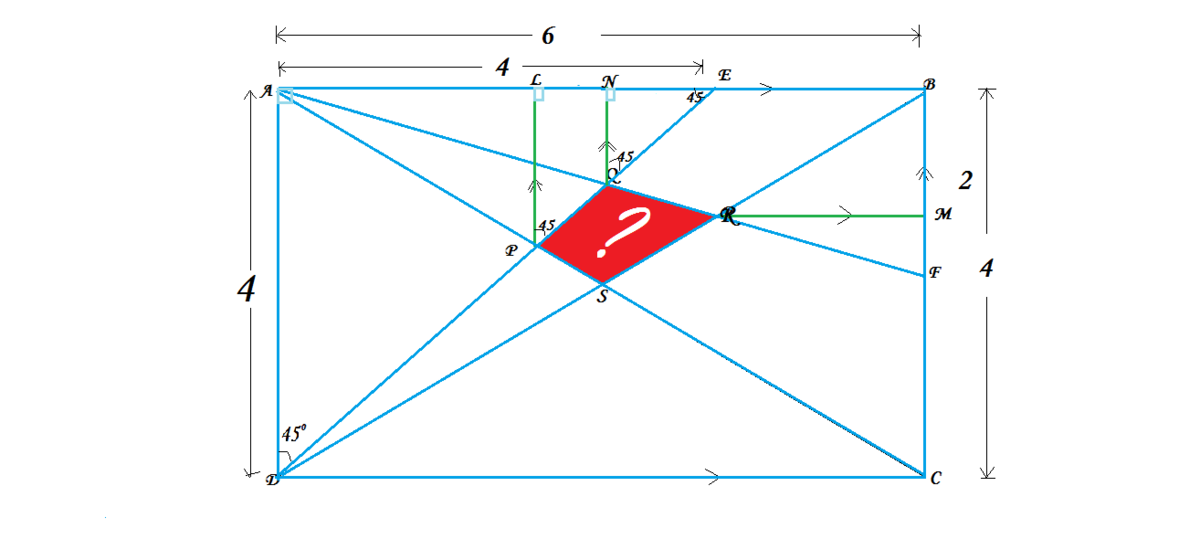
Construction : - Draw PL || BC and QN || BC .
Clearly , PL = LE and QN = NE .............. (1)
Consider △ ANQ and △ ABF,
Clearly they are similar .
.’. A B A N = B F N Q
=> A B A E − N E = B F N Q
=> A B A N − N Q = B F N Q (using 1 )
=> 6 4 − N Q = 2 N Q
=> NQ = 1
.’. Ar . △ AQE = ½ * NQ *AE = ½ * 1 *4 = 2
Consider △ ALP and △ ABC,
Clearly they are similar .
.’. A B A L = B C L P
=> A B A E − L E = B C L P
=> A B A E − L P = B C L P (using 1 )
=> 6 4 − L P = 4 L P
=> LP = 1.6
.’. Ar . △ APE = ½ * LP *AE = ½ * 1.6 *4 = 3.2
Again , Consider △ RMF and △ ABF,
Clearly they are similar .
.’. A B R M = B F M F
=> 6 R M = 2 M F
=> MF = 3 R M ……………….. (2)
Again △ BRM and △ BDC are similar .
.’. D C R M = B C B M
=> 6 R M = 4 B F − M F
=> 6 R M = 4 2 − M F
=> MF = 2- 3 2 R M ………….(3)
From EQ. 2 and EQ . 3 we get
RM = 2
.’. Ar . △BRF = ½ * RM * BF = ½ * 2 * 2 = 2
Also, Ar. △ BSC = ¼ * Ar . rectangle = ¼ * 24 = 6
Again , Ar. △ AFC = ½ * CF * AB = ½ * 2 * 6 = 6
Required area = Ar. △ AFC - Ar . △ APQ - Ar. Quad . SRFC
= 6 - (Ar . △ APE - Ar . △ AQE ) – (Ar. △ BSC- Ar . △BRF )
= 6 – (3.2 -2) –(6-2)
= 6-3.2+2-6+2 = 0.8
Where is Q' in fig. ?
Log in to reply
Q' is on AD so that angle DQ'Q = 90 degrees
Found the coordinates by similar triangles. P(2.4,2.4), R(4,8\3) and Q(3,3), S(3,2).
Since Diagonal QS is vertical base of the two triangles PQS and RQS and Horizontal distance between PQ=1.6, Vertical distance between QS=1.
Area PQRS=
2
1
∗
1
.
6
∗
1
=
0
.
8
.
However the method of Jerry Han Jia Tao is far better for finding coordinate. It is simple and straight.
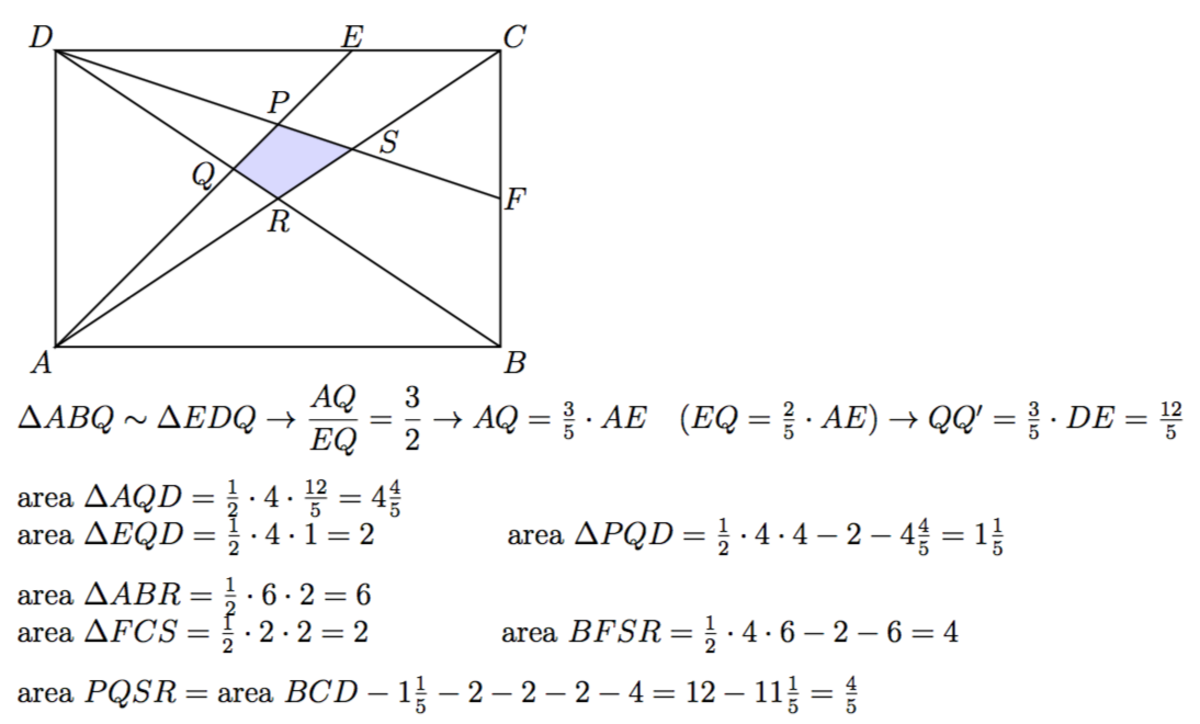
Let:
Equation of DE: y = x
Equation of DB: y = 3 2 x
Equation of AF: y = − 3 1 x + 4
Equation of AC: y = − 3 2 x + 4
Then, we get P = ( 2 . 4 , 2 . 4 ) , Q = ( 3 , 3 ) , R = ( 4 , 3 8 ) , S = ( 3 , 2 )
Now, we can use the shoelace method: [ P Q R S ] = 2 1 ∣ ∣ ∣ ∣ 2 . 4 2 . 4 3 3 4 3 8 3 2 2 . 4 2 . 4 ∣ ∣ ∣ ∣ = 0 . 8