Inspired by Nihar Mahajan
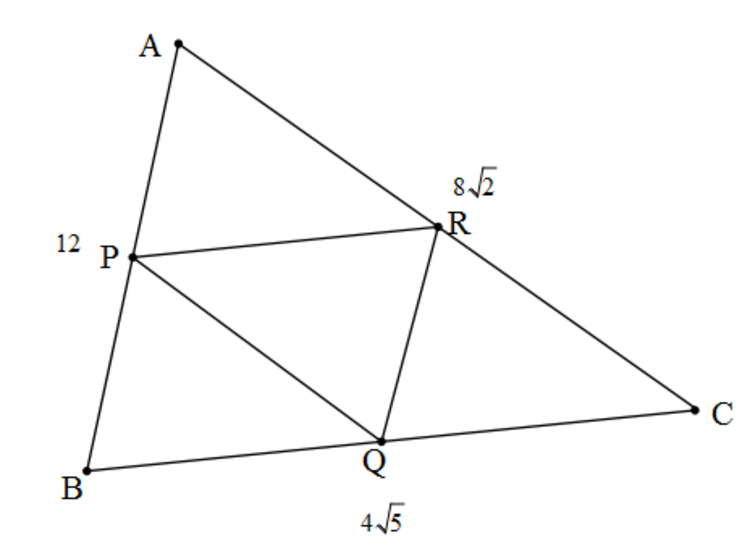 Let
Δ
A
B
C
be a triangle with side
A
B
=
1
2
,
B
C
=
4
5
&
A
C
=
8
2
.
Let
Δ
A
B
C
be a triangle with side
A
B
=
1
2
,
B
C
=
4
5
&
A
C
=
8
2
.
Also let P , Q & R be the points on side A B , B C & C A respectively such that perimeter of Δ P Q R is minimum.
Find the inradius of Δ P Q R .
Note: The picture is not drawn up to scale.
This problem is created by me.
The answer is 1.2648.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
Oh wow! I thought Coordinate Geometry is the only approach. This is terrific!
Log in to reply
Thanks.
Lol , reviewing my old solutions huh? Please review my all 400 solutions :P :P :P
Log in to reply
Haha no, I'm going through a lot of old problems in my bookmark that I haven't had time to solve. You can go through mine as well! ahahahaha
I am posting its solution using Coordinate Geometry and also looking forward for more different type of solution for this question.
Now coming to the solution,
c o s A = 2 b c b 2 + c 2 − a 2 = 2 × 8 2 × 1 2 1 2 8 + 1 4 4 − 8 0 = 2 1 ⟹ A = 4 5 ∘
Now let A be origin. Then B ≡ ( 1 2 , 0 ) & C ≡ ( 8 , 8 )
∴ Line A C ≡ y = x & line B C ≡ 2 x + y = 2 4
Let point P ≡ ( h , 0 ) . We know that minimum perimeter of Δ P Q R would be the distance between the images of point P about line A C & B C .
Images of point P about line A C & B C are D ≡ ( 0 , h ) & E ≡ ( 5 9 6 − 3 h , 5 4 8 − 4 h ) respectively.
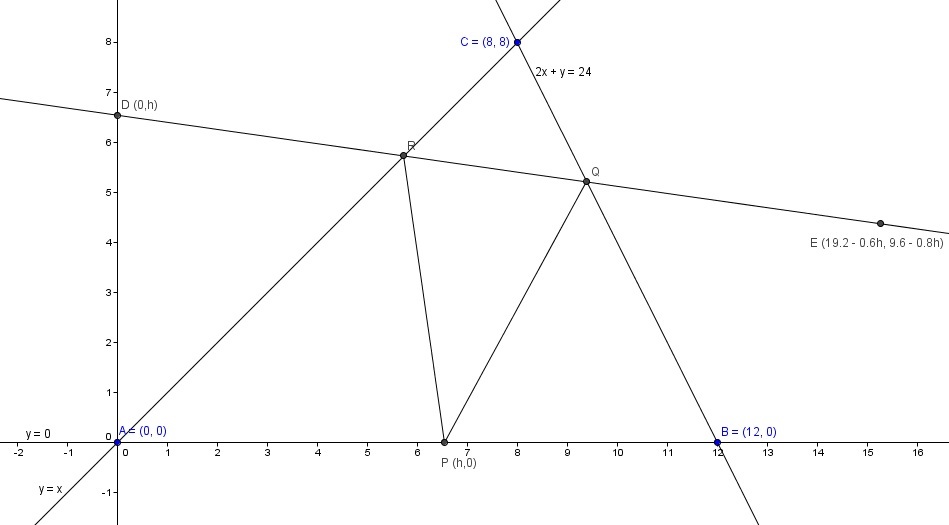
So length of D E = l = 2 5 ( 9 6 − 3 h ) 2 + 2 5 ( 4 8 − 9 h ) 2 ⟹ l 2 = 2 5 ( 9 6 − 3 h ) 2 + 2 5 ( 4 8 − 9 h ) 2 ⟹ 2 l d h d l = 2 5 2 ( 9 6 − 3 h ) × ( − 3 ) + 2 5 2 ( 4 8 − 9 h ) × ( − 9 )
For l to be minimum d h d l = 0 ⟹ − 6 ( 9 6 − 3 h ) = 1 8 ( 4 8 − 9 h ) ∴ h = 8
∴ P ≡ ( 8 , 0 ) , D ≡ ( 0 , 8 ) & E ≡ ( 1 4 . 4 , 3 . 2 )
So line D E ≡ 3 y + x = 2 4 and points Q & R will be point of intersection of line D E with line B C & A C respectively.
∴ Q ≡ ( 9 . 6 , 4 . 8 ) & R ≡ ( 6 , 6 )
Now, area of Δ P Q R = 2 1 × ∣ ∣ ∣ ∣ ∣ ∣ x 1 x 2 x 3 y 1 y 2 y 3 1 1 1 ∣ ∣ ∣ ∣ ∣ ∣ = 9 . 6
And semiperimeter( s ) of Δ P Q R = 2 l = 2 1 5 . 1 8 = 7 . 5 9
∴ Inradius of Δ P Q R = s Δ = 7 . 5 9 9 . 6 ≈ 1 . 2 6 5
Well , I posted another method! ⌣ ¨
Log in to reply
Thanks for your help. It is indeed a great solution.
link text
link text
From the first link we get,
R
=
4
∗
a
r
e
a
a
b
c
=
8
(
1
+
C
o
s
A
∗
C
0
s
B
∗
C
o
s
C
)
a
2
+
b
2
+
c
2
O
r
t
h
i
c
P
e
d
a
l
Δ
h
a
s
m
i
n
i
m
u
m
p
e
r
i
m
e
t
e
r
.
∴
F
r
o
m
s
e
c
o
n
d
.
I
n
r
a
d
i
u
s
o
f
o
r
t
h
i
c
Δ
=
2
R
∗
∣
C
o
s
A
∗
C
o
s
B
∗
C
o
s
C
∣
∴
R
=
(
4
5
+
8
2
+
1
2
)
(
4
5
+
8
2
−
1
2
)
(
4
5
−
8
2
+
1
2
)
(
−
4
5
+
8
2
+
1
2
)
4
5
∗
8
2
∗
1
2
1
+
∣
C
o
s
A
∗
C
o
s
B
∗
C
o
s
C
∣
=
8
∗
R
2
(
4
5
)
2
+
(
8
2
)
2
+
1
2
2
I
n
r
a
d
i
u
s
o
f
o
r
t
h
i
c
Δ
=
2
R
{
8
∗
R
2
(
4
5
)
2
+
(
8
2
)
2
+
1
2
2
−
1
}
=
1
.
2
6
4
9
.
H is the Orthocenter of ABC
Well , This is a pure geometry proof. I think the problem poser is inspired by this problem . The triangle with minimum perimeter is indeed the orthic triangle of Δ A B C (this can be proved). Please revise the orthic configuration before seeing this proof , or you will not understand some steps.I t almost took 2 hours for me to solve and present the solution. Do upvote if you like.
First by Heron's formula we can compute that : A ( Δ A B C ) = 4 8
A ( Δ A B C ) = 2 1 ( A B ) ( P C ) = 2 1 ( 1 2 ) ( P C ) = 4 8 ⇒ P C = 8 A C = 8 2 m ∠ C P A = 9 0 ⇒ Δ C P A is a 45-45-90 triangle ⇒ A P = 8
By angle chase we also see that Δ C P A is also a 45-45-90 triangle.
⇒ A R = 6 2 , P B = A B − A P = 1 2 − 8 ⇒ P B = 4 Also , R C = A C − A R = 8 2 − 6 2 = 2 2
By Pythagoras Theorem to Δ A B Q , we get B Q = 5 1 2 5 Q C = B C − B Q = 4 5 − 5 1 2 5 ⇒ Q C = 5 8 5
Now since we have computed all the parts of sides of Δ A B C ,we can use ratios and computations to get P Q , Q R , P R .
Δ A P R ∼ Δ A C B ⇒ A C A P = C B P R ⇒ P R = 2 1 0 Δ B P Q ∼ Δ B C A ⇒ B C B P = C A P Q ⇒ P Q = 5 8 1 0 Δ C R Q ∼ Δ C B A ⇒ B C C R = B A Q R ⇒ Q R = 5 6 1 0
For Δ P Q R , semiperimeter s = 5 1 2 1 0
Also by heron's formula , we find A ( Δ P Q R ) = 5 4 8
Hence , inradius r = s A ( Δ P Q R ) = 5 1 2 1 0 5 4 8 = 5 2 1 0
⇒ r = 5 2 1 0 ≈ 1 . 2 6 5