Inspired by Otto Bretscher and Abhay Tiwari

Calculus Level pending

$\huge x^{x^{x^{x^{.^{.^{x^{n}}}}}}}=2$

The above power tower can be viewed as a recurrence relation: $a_0=n, a_{k+1}=x^{a_{k}}$ for $k \ge 0$ and $\displaystyle\lim_{k \to \infty}a_k=2$ .

It is known that $n$ is a constant and $x=\sqrt{2}$ is the solution of the above equation. What is the largest range for $n$ ?

n \in (-\infty, \infty )

n=\sqrt{2}

n \in (-\infty, 0)

n \in (-\infty, 4)

n \in (0, \infty)

n \in (-\sqrt{2}, \sqrt{2})

n \in (0, 4)

n \in (0, \sqrt{2})

1 solution

Chan Lye Lee
May 9, 2016

Here are the graphs showing iteration of $a_k$ for (i) $n <2$ , (ii) $2 <n<4$ and (iii) $n>4$ respectively.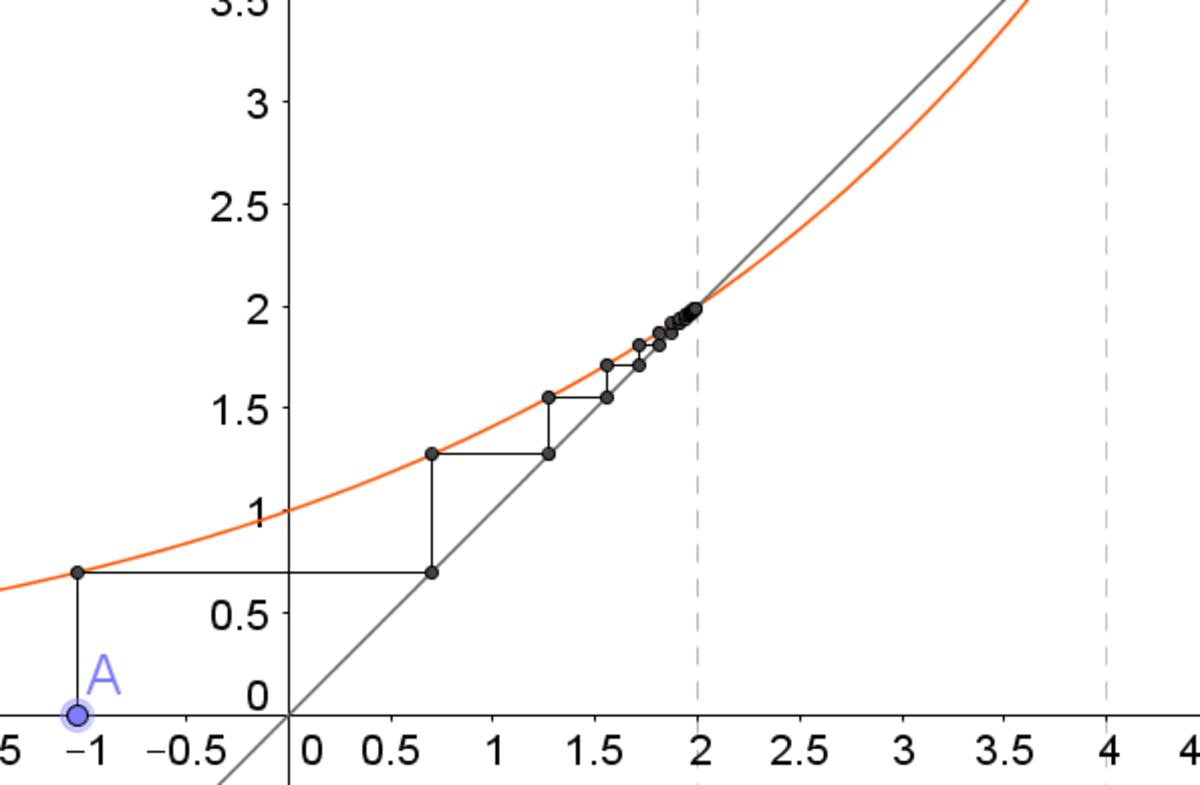

We can get the idea from here that the $\displaystyle \lim_{k \to \infty} a_k=2$ for all $n<4$ .

Any good algebraic proof?