Inspired by Pi Han Goh
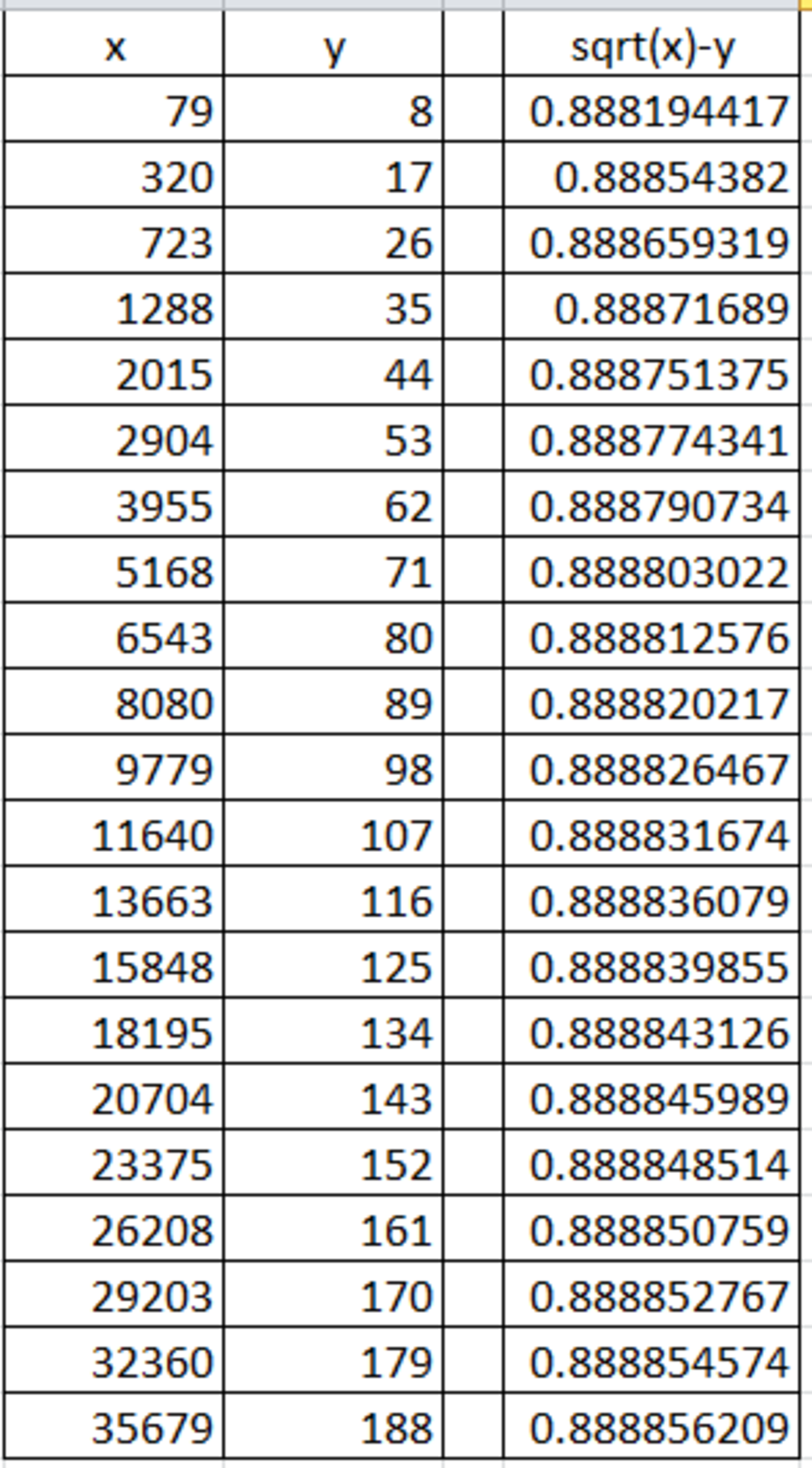
Note that 7 9 − 8 ≈ 0 . 8 8 8 and 3 2 0 − 1 7 ≈ 0 . 8 8 8 in the sense that the first 3 decimal places of these two numbers are equal.
Now we see that ⌊ 1 0 0 0 ( 7 9 − 8 ) ⌋ = ⌊ 1 0 0 0 ( 3 2 0 − 1 7 ) ⌋ = 8 8 8 .
Suppose ⌊ 1 0 0 0 ( x − y ) ⌋ = 8 8 8 where x , y are positive integers and x > 3 2 0 . What is the minimum value of x + y ?
The answer is 749.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
That is a nice pattern. I used a bit of brute force and looked for the next integer y such that ( y + 0 . 8 8 8 ) 2 and ( y + 0 . 8 8 9 ) 2 straddled an integer x , and was fortunate that I only had to go up to y = 2 6 .
In the problem, can you clarify what you mean by ≈ 0 . 8 8 8 ? This would help with understanding your intentions. My concerns are
- There are values of x, y that will return (say) ≈ 0 . 8 8 8 3 (though with a larger sum).
- I could argue that 7 2 3 − 2 6 ≈ 0 . 8 8 9 instead.
What you have is a great pattern! If you want to approximate ( y + 9 8 ) 2 as an integer, then yes setting y = 9 n − 1 works out great and we're just off by 8 1 1 .
This is a partial solution.
There is a nice pattern for integers x and y so that x − y ≈ 0 . 8 8 8 .
The pattern is as follows: x 1 = 7 9 , x n = ⌈ ( x n − 1 + 9 ) 2 ⌉ for all n ≥ 2 .
y n = 9 n − 1 .
After @Calvin Lin's comment: Here is a better way to understand: x n = ⌊ ( 9 n − 9 1 ) 2 ⌋ .
From the table below, the next value of x after 320 is 723, and the corresponding y is 26. So x + y = 7 2 3 + 2 6 = 7 4 9 .
(This solution is yet completed as we have not proved that 749 is the minimum value of x + y .)
Now you may want to prove that lim n → ∞ ( x n − y n ) = 9 8 = 0 . 8 8 8 8 8 8 8 8 8 8 8 8 . . .