Inspired by problem 3, IMO 1973

$P(x)=x^4+ax^3+x^2+bx+1=0$ Let $S$ be the set of pairs of real numbers $(a, b)$ at which $P(x)=0$ has at list one real root. It's immediate that $S'=A$ , where $S'$ is the complement of set $S$ . We claim that for each point on boundary $f$ of set $S$ like $(a_0, b_0)$ the equation $P(x)=0$ has at least one multiple root. Because if all the roots of $P(x)=0$ at point $(a_0, b_0)$ be simple, there is a neighborhood of this point where all of roots of $P(x)=0$ are also simple (Because if changes in coefficients are small enough, changes in roots will be very small as well and they remain simple). Therefore, $(a_0, b_0)$ would be a interior point of $S$ and not a boundary point of it. So for each point on $f$ , the equation $P(x)=0$ has at least one multiple root. This conclusion was enough for solving my previous problem ,but here we need more. I want to conclude that we have no simple root on $f$ .

Another point of view for type of roots on boundary is that in fact set $A$ has no boundary. Actually when $P(x)=0$ has only complex roots, graph of $P(x)$ in the $x$ - $y$ plane can approach $x$ -axis most tightly, but it can't touch it. When $P(x)$ touches the $x$ -axis we're on the boundary of set $S$ and $P(x)$ is tangent to $x$ -axis at some point $(a_0, b_0)$ , so we have only multiple roots in this point (This is a general rule for problems like this). Now, we want to obtain the shape of $f$ :

Let $r \neq 0$ be one of real multiple roots of the polynomial in some point $(a_0, b_0)$ of $f$ , then $\displaystyle \begin{array}{c}\\ P(x) &&=x^4+ax^3+x^2+bx+1=(x-r)^2 \left(x^2+s x +\frac{1}{r^2} \right) \\ &&= x^4+(s-2r)x^3+ \left( r^2+\frac{1}{r^2}-2sr \right) x^2 +\left( sr^2-\frac{2}{r} \right) x+1 \end{array}$ Thus, $s-2r=a \\ r^2+\frac{1}{r^2}-2sr =1 \\ sr^2-\frac{2}{r}=b$ Combining last three relations, one can get $s=\frac{1}{2r}\left( r^2+\frac{1}{r^2}-1 \right)$ $f(r) =\left\{\begin{array}{lr} a(r)=\frac{1}{2r}\left( r^2+\frac{1}{r^2}-1 \right)-2r \\ b(r)=\frac{r}{2}\left( r^2+\frac{1}{r^2}-1 \right)-\frac{2}{r} \end{array} \right.$ Note that there are no simple roots on $f$ so discriminant of quadratic $x^2+sx+\frac{1}{r^2}$ must be less than or equal to zero, this means $s^2-\frac{4}{r^2} \le 0$ or: $s^2 \le \frac{4}{r^2} \\ \frac{1}{4r^2}\left( r^2+\frac{1}{r^2}-1 \right)^2 \le \frac{4}{r^2} \\ \left( r+\frac{1}{r} \right)^2 \le 7 \\ 2 \le \left| r+\frac{1}{r} \right| \le \sqrt{7}$ Hence we get the domain of $f$ as $r \in \left\{ \left [-\frac{1}{r^{\star}}, -r^{\star} \right ] \cup \left [r^{\star}, \frac{1}{r^{\star}} \right ]\right\}$ Where $r^{\star}=\frac{\sqrt{7}-\sqrt{3}}{2}$ . Let's plot $S$ , $f$ and $A$

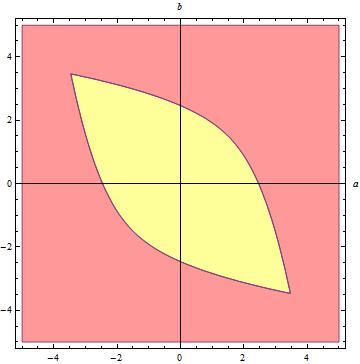
Red part of the graph and the boundary $f$ (black) form set $S$ and yellow part is $A$ where all of the roots of $P(x)=0$ are complex (why?). Let us use some calculus to find area of $A$ . We have a complete symmetric system for $f$ . Since domain of $f$ is symmetric with respect to origin in parameter space and $a(-r)=-a(r)$ and $b(-r)=-b(r)$ we get $\text{Area}= 2\left| \int_{r^{\star}}^{\frac{1}{r^{\star}}} a(r) b'(r) \ \text{d}r \right|$ (why?). You may integrate above integral to get $\text{Area}=\frac{19\sqrt{21}}{4}+ 5 \ \tanh ^{-1} \left( \sqrt{\frac{3}{7}} \right)$ We are done.