Inspired by Tad
Consider the rectangular spiral in the image below. It starts from the origin and twirls and twirls forever in an anticlockwise direction along the integer coordinates of the Cartesian coordinate plane. Each point along the spiral is numbered with an integer Z as shown in the image below.
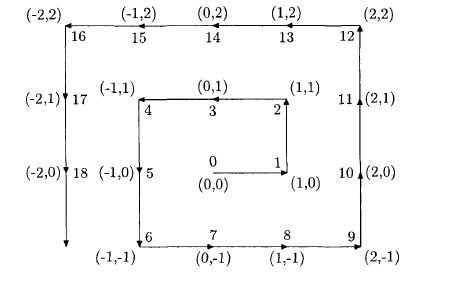
Let f ( Z ) be the sum of x and y coordinate of the point numbered Z . What is the value of f ( 6 6 6 4 0 0 1 ) + f ( 8 8 7 5 1 7 2 ) + f ( 4 8 2 0 6 6 9 ) ?
Clarification
As an explicit example, the point Z = 3 is ( 0 , 1 ) , hence f ( 3 ) = 0 + 1 = 1 .
The answer is 4920.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
can you please explain how did you arrived at finding P(x)?
Log in to reply
Look at the pattern. Starting at the origin, the line moves 1 right, 1 up, 2 left 2 down (total of 6), 3 right, 3 up, 4 left 4 down (total of 14, so now have had 20 moves), 5 right, 5 up, 6 left, 6 down (total of 22, so now we have had 42 moves), and so on.
Thus the n th stage of this process (starting with n = 0 ) involves moving 2 n + 1 right, 2 n + 1 up, 2 n + 2 left, 2 n + 2 down. There have been 2 n ( 2 n + 1 ) moves already, so by the end of the n th stage there have been 2 n ( 2 n + 1 ) + 2 ( 2 n + 1 ) + 2 ( 2 n + 2 ) = ( 2 n + 2 ) ( 2 n + 3 ) moves. The n th stage specifies P ( 2 n ( 2 n + 1 ) + j ) for 1 ≤ j ≤ 8 n + 6 although, for convenience, and to include the starting p[oint ( 0 , 0 ) , the final move of any stage is shown as the starting j = 0 position of the following stage.
Solution implemented in python 3
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 |
|
Output
1 |
|
As a programming problem:
δ = ⎝ ⎜ ⎜ ⎛ 1 0 − 1 0 0 1 0 − 1 ⎠ ⎟ ⎟ ⎞
interesting = { 6 6 6 4 0 0 1 , 8 8 7 5 1 7 2 , 4 8 2 0 6 6 9 }
max = max ( interesting )
position = { 0 , 0 } ; direction = 0 ; distance = 1 ; step = distance ; z = − 1 ; first = True ; While [ z ≤ max , ++ z ; If [ MemberQ [ interesting , z ] , Print [ { z , position , Plus @@ position } ] ] ; position = δ [ [ direction + 1 ] ] + position ; – step ; If [ step = 0 , direction = ( ( direction + 1 ) m o d 4 ) ; If [ ¬ first , ++ distance ] ; first = ¬ first ; step = distance ; ] ]
We can find a pattern in the top-left corners of the diagram. Their numbers count 0 , 4 , 1 6 , 3 6 , 6 4 , 1 0 0 . . . , which are the squares of even numbers 0 2 , 2 2 , 4 2 , 6 2 , 1 0 2 . . . . Now, if we find the biggest even square S less than Z , then the coordinates of the point S will be ( − 2 1 S , 2 1 S ) . Starting at this point we move around the rectangle for ( Z − S ) moves and get to the point Z .
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 |
|
1 2 |
|
The pattern of the spiral (right 1, up 1, left 2, down 2, right 3, up 3, left 4, down 4, right 5, up 5, left 6, up 6, ...) is easy to solve. The N th point has coordinates P ( N ) , where P ( 2 n ( 2 n + 1 ) + j ) = ⎩ ⎪ ⎪ ⎨ ⎪ ⎪ ⎧ ( − n + j , − n ) ( n + 1 , j − 3 n − 1 ) ( 5 n + 3 − j , n + 1 ) ( − n − 1 , 7 n + 5 − j ) 0 ≤ j ≤ 2 n + 1 2 n + 2 ≤ j ≤ 4 n + 2 4 n + 3 ≤ j ≤ 6 n + 4 6 n + 5 ≤ j ≤ 8 n + 5 for all n ≥ 0 . Thus, for n ≥ 0 , f ( 2 n ( 2 n + 1 ) + j ) = { j − 2 n 6 n + 4 − j 0 ≤ j ≤ 4 n + 2 4 n + 3 ≤ j ≤ 8 n + 5 We calculate N 6 6 6 4 0 0 1 8 8 7 5 1 7 2 4 8 2 0 6 6 9 n 1 2 9 0 1 4 8 9 1 0 9 7 j 5 0 2 1 3 7 1 0 4 8 3 9 f 2 4 4 1 7 3 2 1 7 4 7 making the answer 4 9 2 0 .