Inspired by Twinkle Twinkle Little Star
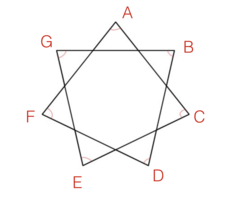 Find the value of
A
+
B
+
C
+
D
+
E
+
F
+
G
in degrees.
Find the value of
A
+
B
+
C
+
D
+
E
+
F
+
G
in degrees.
The answer is 540.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
Generalisation: Given an n-pointed star, the sum of the angles at the points is 180*(n-4)
Log in to reply
Shame on me, I have kind of invented a complex formula : 180 - 2(180 - (180 -360 : n )) * n where n is the amount of angles of the polygon. I should have simplified it...
I used the same method.
Here is my approach:
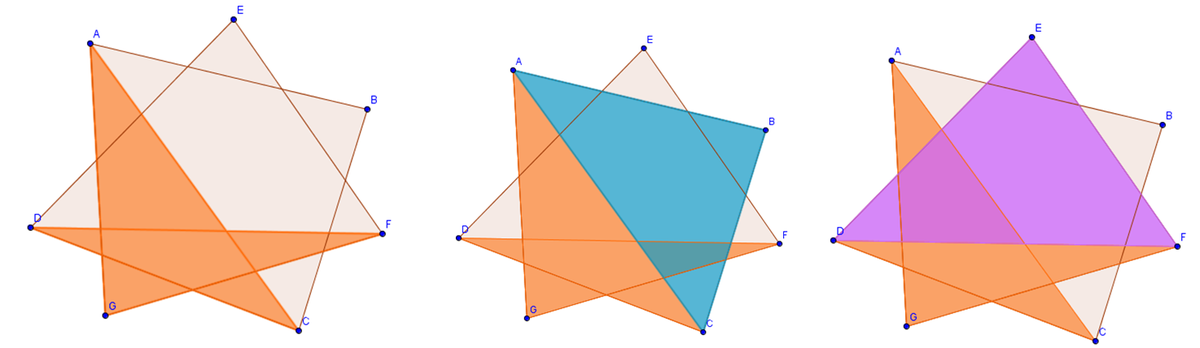
It is easy to show that the sum of angles in '5-star' is 180 degrees, then the other two triangles has angle sum 180 degrees each. Hence the answer.
Travel through the diagram from A back to A. It is clear that you make two complete loops around the center, so that you turned 2 ⋅ 3 6 0 ∘ .
The marked angle at each turn is 1 8 0 ∘ − the angle over which you turn when traveling around.
Therefore, 2 ⋅ 3 6 0 ∘ = 7 ⋅ X = A , … , G ∑ ( 1 8 0 ∘ − ∠ X ) = 7 ⋅ 1 8 0 ∘ − ( A + ⋯ + G ) . Solve this to find A + ⋯ + G = 7 ⋅ 1 8 0 − 2 ⋅ 3 6 0 = 5 4 0 ∘ .
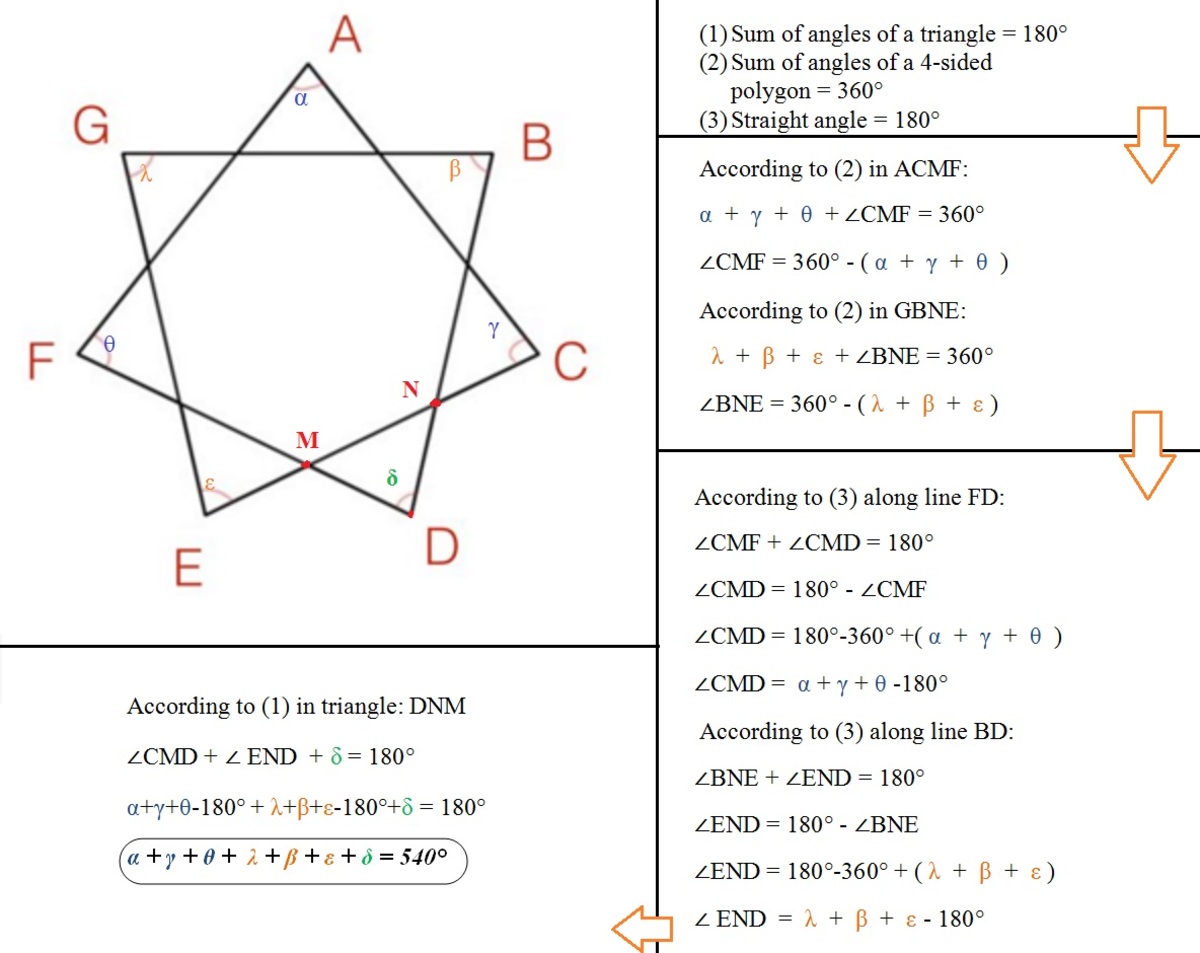
Using Vertical Angles and Triangles - Exterior Angles , we can see:
Using Regular Polygons - Angle Sum , the internal heptagon (outlined in blue) has a sum of angles equal to 5 ⋅ 1 8 0 degrees. However, each of its angles is in the form 1 8 0 − a , for a total sum of 1 8 0 ⋅ 7 − ( a + b + c + d + e + f + g ) , so a + b + c + d + e + f + g = 2 ⋅ 1 8 0 .
Each of the angles we want to add up is in the form 1 8 0 − a − b , and each variable is included in two triangles. Thus, the entire sum is 1 8 0 ⋅ 7 − 2 ( a + b + c + d + e + f + g ) = 1 8 0 ⋅ 7 − 2 ⋅ 2 ⋅ 1 8 0 = 3 ⋅ 1 8 0 = 5 4 0 .
Remark: There are many clever ways to approach this problem (e.g., the "pencil rolling" approach), and the result can be generalized. How did you solve it? Post your solution!