Magic Square With Minimal Information
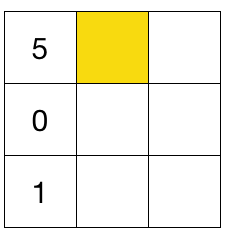
In the above magic square, all the rows, columns and diagonals each sum up to 6.
What is the entry of the square shaded in yellow?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
Let the elements of the magic square be a , b , c , d , e , f .
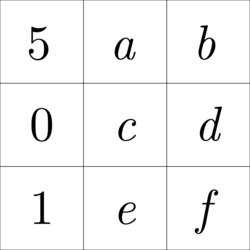
The sum of every row, column, and diagonal is 6. We can write these sums as a system of linear equations. Let's look at the row sums first:
5 + a + b = 6 0 + c + d = 6 1 + e + f = 6 ⟹ b = 1 − a d = 6 − c f = 5 − e
We can eliminate b , d , and f from the magic square by writing them in terms of a , c , and e .

The sum of second column is 6. We get a + c + e = 6 . Therefore, e = 6 − a − c . We can eliminate e from the magic square by writing it in terms of a and c .
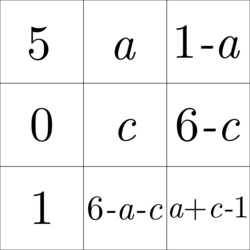
The sum of the diagonals is also 6.
5 + c + ( a + c − 1 ) = 6 ( 1 − a ) + c + 1 = 6 ⟹ a + 2 c = 2 − a + c = 4
When we add the two equations, we get 3 c = 6 . Substituting back c = 2 in the equation gives us a = − 2 . When we substitute values of a and c in the magic square, we get

The number that goes in the yellow square is − 2 .
This is a consistent solution since the sum of each row, column and diagonal is 6 . This is also a unique solution as the solving the linear equation gave us this solution only.
How did you obtain this configuration? How do you know the answer is unique?
There is no number. How did you know ?
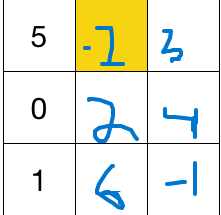
Proof: Let the numbers in the square be a , b , c , d , e , f , g , h , i from left to right, top to bottom. Let the magic sum be S. We have S = a + e + i , S = b + e + h , S = c + e + g . Also, we have S = a + b + c and S = g + h + i . Summing up the first 3 equations and subtracting the last 2, we get S = 3 e .
In this problem, since the magic sum is S = 5 + 0 + 1 = 6 , so
the center center square is 3 6 = 2 ,
the lower right square is 6 − 5 − 2 = − 1 ,
the lower center square is 6 − 1 − ( − 1 ) = 6 ,
the upper center square is 6 − 6 − 2 = − 2 .
Note: We can show that the upper right square is 6 − 5 − ( − 2 ) = 3 and the center right square is 6 − 0 − 2 = 4 .