Inspired by(copied from) IGSCE

Geometry Level 4

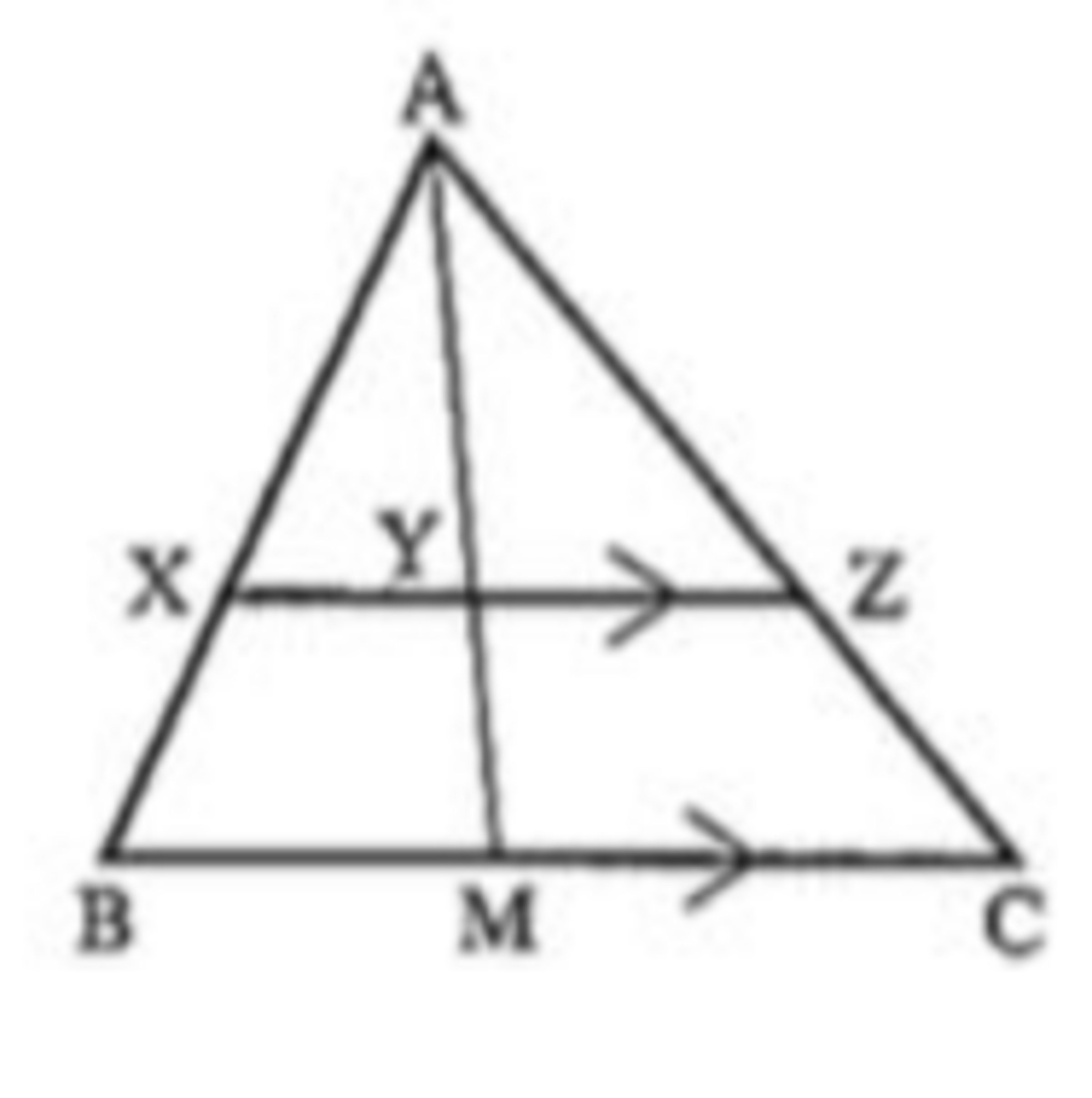
Given that A Z = 3 cm , Z C = 2 cm , M C = 5 cm , B M = 3 cm AZ = 3\text{ cm}, ZC = 2\text{ cm}, MC=5\text{ cm}, BM=3\text{ cm} and X Y Z ∣ ∣ B M C XYZ||BMC . If the ratio of the areas of the triangles, [ A X Y ] [ A Y Z ] \dfrac{[AXY]}{[AYZ]} is a b \dfrac ab , where a a and b b are coprime positive integers, find a + b a+b .


The answer is 8.

Aareyan Manzoor by Aareyan Manzoor , 18, USA

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

3 solutions

Thale's theorem in Δ A M C \Delta AMC : Y Z M C = A Z A C = 3 5 ⇒ Y Z = 5 × 3 5 = 3 c m \dfrac{YZ}{MC} = \dfrac{AZ}{AC} = \dfrac{3}{5} \Rightarrow YZ = 5 \times \dfrac{3}{5} = \boxed{3 cm} .

Thale's theorem in Δ A B M \Delta ABM : X Y B M = A X A B = 3 5 ⇒ X Y = 3 × 3 5 = 9 5 c m \dfrac{XY}{BM} = \dfrac{AX}{AB} = \dfrac{3}{5} \Rightarrow XY = 3 \times \dfrac{3}{5} = \boxed{\dfrac{9}{5} cm} .

Now, a r ( A X Y ) a r ( A Y Z ) = X Y Y Z \dfrac{ar(AXY)}{ar(AYZ)} = \dfrac{XY}{YZ} [Since they have common altitude] = 3 5 = \boxed{\dfrac{3}{5}} .

3 Helpful 0 Interesting 0 Brilliant 0 Confused

or you could use a r e a = a b 2 sin ⁡ ( θ ) area=\dfrac{ab}{2} \sin(\theta) Nice sol(+1).

Aareyan Manzoor - 5 years, 2 months ago

Log in to reply

I wanted the solution to be accessible to a wider lot, so didn't involve trig here. Thanks !

Venkata Karthik Bandaru - 5 years, 2 months ago

LOL, values of A Z AZ and Z C ZC are not required!

Nihar Mahajan - 5 years, 2 months ago
Nihar Mahajan
Apr 12, 2016

Since X Z ∣ ∣ B C XZ \ || \ BC , we have X Y B M = Y Z M C = A Y A M ⟹ X Y Y Z = B M M C = 3 5 ⟹ [ A X Y ] [ A Y Z ] = 3 5 \dfrac{XY}{BM}=\dfrac{YZ}{MC}=\dfrac{AY}{AM} \implies \dfrac{XY}{YZ}=\dfrac{BM}{MC}=\dfrac{3}{5} \implies \boxed{\dfrac{[AXY]}{[AYZ]}=\dfrac{3}{5}} .

2 Helpful 0 Interesting 0 Brilliant 0 Confused

Moderator note:

Why is the condition " X Y B M = Y Z M C = A Y A M \dfrac{XY}{BM}=\dfrac{YZ}{MC}=\dfrac{AY}{AM} " necessary? Can't we immediately do X Y ∥ B C ⇒ 3 5 = B M M C = X Y Y Z = [ A X Y ] [ A Y Z ] XY \parallel BC \Rightarrow \dfrac{3}{5}=\dfrac{BM}{MC}=\dfrac{XY}{YZ}=\dfrac{[AXY]}{[AYZ]} ?

X Y Z ∣ ∣ B M C ∴ Δ A X Y Δ A B M , Δ A Y Z Δ A M C . ∴ X Y Y Z = B M M C = 3 5 = ratio of bases of Δ s A X Y a n d A X Z . Since the heights of these triangles is same, their areas are in proportion of there bases. T h a t i s 3 5 . ⟹ a + b = 8. XYZ ~|| ~BMC~~~~~~~~~\therefore~ \Delta ~AXY\text{~} \Delta ~ABM ,~~~~~\Delta ~AYZ\text{~} \Delta ~AMC .\\ \therefore~\dfrac{XY}{YZ}=\dfrac{BM}{MC}=\dfrac 3 5=\text{ratio of bases of } \Delta s ~AXY~and ~AXZ.\\ \text{Since the heights of these triangles is same, their areas are in proportion of there bases. }\\ That ~~ is~~ \frac 3 5.~~~\implies~a+b=8.

0 Helpful 0 Interesting 0 Brilliant 0 Confused

How did you assume XYZ ll BMC?

Silver Vice - 5 years, 2 months ago

Log in to reply

You are right. From the sketch we took ||. But it should have been specified.

Niranjan Khanderia - 5 years, 1 month ago

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...